Superconductivity

Bardeen, Cooper and Schrieffer’s (BCS) theory of superconductivity
Idea: electrons bind to form Cooper pairs that behave like bosons
The phenomena of superconductivity and superfluidity are closely linked: superconductor is ‘like’ BEC of Cooper pairs

Same Hamiltonian as before

H = \int d\mathbf{r}\left[ \sum_{s=\uparrow,\downarrow}\frac{1}{2m}\nabla\psi^\dagger_s\cdot\nabla\psi^{\vphantom{\dagger}}_s + U_0 \psi^\dagger_\uparrow\psi^\dagger_\downarrow\psi^{\vphantom{\dagger}}_\downarrow\psi^{\vphantom{\dagger}}_\uparrow\right]

For a pair of particles of opposite spin, this is equivalent to

H = -\frac{1}{2m}\left[\nabla_1^2+\nabla_2^2\right] + U_0\delta(\mathbf{r}_1-\mathbf{r}_2)

For U_0<0 and sufficiently large, expect a bound state to form with a symmetric spatial wavefunction and a spin singlet

Check

Discussion: Cooper’s problem

The BCS Wavefunction

In momentum space our Hamiltonian is

H =\sum_{\mathbf{k},s} \epsilon(\mathbf{k})a^\dagger_{\mathbf{k},s}a^{\vphantom{\dagger}}_{\mathbf{k},s} + \overbrace{\frac{U_0}{V}\sum_{\mathbf{k}_1+\mathbf{k}_2=\mathbf{k}_3+\mathbf{k}_4} a^\dagger_{\mathbf{k}_1,\uparrow}a^\dagger_{\mathbf{k}_2,\downarrow}a^{\vphantom{\dagger}}_{\mathbf{k}_3,\downarrow}a^{\vphantom{\dagger}}_{\mathbf{k}_4,\uparrow}}^{\equiv H_\text{int}}

Take interaction between the two species to be attractive U_0<0
Ground state of non-interacting problem is

\lvert{\text{FS}}\rangle=\prod_{|\mathbf{p}|<k_\text{F}} a^\dagger_{\mathbf{p}\uparrow}a^\dagger_{-\mathbf{p}\downarrow}\lvert{\text{VAC}}\rangle.

Application of interaction Hamiltonian H_\text{int} generates terms of form a^\dagger_{\mathbf{p}+\mathbf{q}\uparrow}a^\dagger_{-\mathbf{p}\downarrow}a^{\vphantom{\dagger}}_{-\mathbf{p}'\downarrow}a^{\vphantom{\dagger}}_{\mathbf{p}'+\mathbf{q}\uparrow}\lvert{\text{FS}}\rangle with |\mathbf{p}|,|\mathbf{p}+\mathbf{q}|>k_\text{F},|\mathbf{p}'|,|\mathbf{p}'+\mathbf{q}|<k_\text{F}

Note difference from Bose case: don’t just create pair excitations with zero centre of mass momentum \mathbf{q}=0
Nevertheless, BCS theory makes assumption that ground state involves a superposition of zero momentum pairs only
We can write such a state very generally as

\lvert{\text{pair}}\rangle\equiv\sum_{\sum_\mathbf{p}n^P_\mathbf{p}=N/2} c_{\{n^P_{\mathbf{p}}\}} \prod_{\mathbf{p}}\left[a^\dagger_{\mathbf{p}\uparrow}a^\dagger_{-\mathbf{p}\downarrow}\right]^ {n_{\mathbf{p}}}\lvert{\text{VAC}}\rangle

Restricting ourselves to states of this form means that

\Braket{\text{pair}|H_\text{int}|\text{pair}} = \frac{U_0}{V}N_\uparrow N_\downarrow+\Braket{\text{pair}|\tilde H_{\text{int}}|\text{pair}}

First term is the Hartree–Fock energy and

\tilde H_{\text{int}}=\frac{U_0}{V}\sum_{\mathbf{p}, \mathbf{p}'}a^\dagger_ {\mathbf{p}\uparrow}a^\dagger_{-\mathbf{p}\downarrow}a^{\vphantom{\dagger}}_{-\mathbf{p}'\downarrow}a^{\vphantom{\dagger}}_{\mathbf{p}'\uparrow}

Check

Why? There is some double counting of terms that is irrelevant as V\to\infty

Introduce the pair operators b^\dagger_\mathbf{p}=a^\dagger_{\mathbf{p}\uparrow}a^\dagger_{-\mathbf{p}}, b^{\vphantom{\dagger}}_\mathbf{p}=a^{\vphantom{\dagger}}_{-\mathbf{p},\downarrow}a^{\vphantom{\dagger}}_{\mathbf{p}\uparrow}
For \Braket{\text{pair}|\cdots|\text{pair}} we can replace H\to H_\text{pair} H_{\text{pair}}=2\sum_{\mathbf{p}}\epsilon_{\mathbf{p}}b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}+\frac{U_0}{V}\sum'_{\mathbf{p},\mathbf{p}'} b^\dagger_\mathbf{p} b^{\vphantom{\dagger}}_{\mathbf{p}'} since 2b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}= a^\dagger_{\mathbf{p},\uparrow}a^{\vphantom{\dagger}}_{\mathbf{p},\uparrow}+a^\dagger_{-\mathbf{p},\downarrow}a^{\vphantom{\dagger}}_{-\mathbf{p},\downarrow} on these states
Looks quadratic. Can we solve it?

Nope! b^\dagger_\mathbf{p}, b^{\vphantom{\dagger}}_\mathbf{p} don’t obey canonical Bose commutation relations
Pair operators b^{\vphantom{\dagger}}_\mathbf{p} commute at different momenta [b^{\vphantom{\dagger}}_\mathbf{p},b^{\vphantom{\dagger}}_{\mathbf{p}'}]=[b^\dagger_\mathbf{p},b^\dagger_{\mathbf{p}'}]=[b^\dagger_\mathbf{p},b^{\vphantom{\dagger}}_{\mathbf{p}'}]=0\qquad \mathbf{p}\neq\mathbf{p}', but obey the hardcore constraint

(b^\dagger_\mathbf{p})^2=0 (can’t create two fermions in same state)

Try variational state (pair amplitudes factorize c.f. Bogoliubov)

\lvert{N \text{ pair}}\rangle\equiv\left[\sum_\mathbf{p}c_\mathbf{p}b^\dagger_\mathbf{p}\right]^{N/2}\lvert{\text{VAC}}\rangle

Energy expectation still tricky. For instance, what is the expectation value of the kinetic energy?

\mathrm{K.E}=2\sum_\mathbf{p}\epsilon_{\mathbf{p}}\langle b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}\rangle\equiv 2\sum_\mathbf{p}\epsilon_{\mathbf{p}} \langle n^P_ \mathbf{p}\rangle,

Finding average number of pairs \langle n^P_\mathbf{p}\rangle not obvious

BCS considered normalized wavefunction

\lvert{\text{BCS}}\rangle =\prod_\mathbf{p}\left[v_\mathbf{p}b^\dagger_\mathbf{p}+u_\mathbf{p}\right]\lvert{\text{VAC}}\rangle\qquad |u_\mathbf{p}|^2+|v_\mathbf{p}| ^2=1.

Superposition of states with different total number of particles

Check

Projection to fixed number N of particles matches \lvert{N \text{ pair}}\rangle\equiv\left[\sum_\mathbf{p}c_\mathbf{p}b^\dagger_\mathbf{p}\right]^{N/2}\lvert{\text{VAC}}\rangle if c_\mathbf{p}=v_\mathbf{p}/u_\mathbf{p}.

\langle n^P_\mathbf{p}\rangle= v_\mathbf{p}^2 and total variational energy of this state is

\Braket{\text{BCS}|H|\text{BCS}}=2\sum_\mathbf{p}\epsilon_{\mathbf{p}}|v_\mathbf{p}|^2+\frac{U_0}{V}\sum_{\mathbf{p},\mathbf{p}'}u^*_\mathbf{p}v_ \mathbf{p}u_{\mathbf{p}'}v^*_{\mathbf{p}'}

Check

Show this

How about that non-conserving wavefunction?

Expectation of any particle number conserving operator is

\Braket{\text{BCS}|\mathcal{O}|\text{BCS}}=\sum_N P_N \Braket{N \text{ pair}|\mathcal{O}|N\text{ pair}}

The probabilities P_N are

P_N=\sum_{\sum n^P_\mathbf{p}=N/2}\prod_\mathbf{p}\left[n^P_\mathbf{p}|v_\mathbf{p}|^2+\left(1-n^P_\mathbf{p}\right)|u_\mathbf{p}|^2 \right]

Distribution strongly peaked around

\langle N \rangle=2\sum_\mathbf{p}|v_\mathbf{p}|^2=2\sum_\mathbf{p}\langle n^P_\mathbf{p} \rangle with a variance that is O(N). Thus at large N

\Braket{\text{BCS}|\mathcal{O}|\text{BCS}}\to \Braket{\langle N\rangle \text{ pair}|\mathcal{O}|\langle N\rangle\text{ pair}}

Anderson spin chain

b^{\vphantom{\dagger}}_\mathbf{p}, b^\dagger_\mathbf{p}, and b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}-1/2 behave as the components of a spin-1/2 S_\mathbf{p}^+ \equiv b^\dagger_\mathbf{p},\quad S_\mathbf{p}^- \equiv b^{\vphantom{\dagger}}_\mathbf{p},\quad S^z_\mathbf{p}= b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}-1/2, on account of the commutation relations (Anderson spins)

\begin{aligned} \left[b^\dagger_\mathbf{p},b^{\vphantom{\dagger}}_\mathbf{p}\right]=2\left(b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}-1/2\right)\nonumber\\ \left[b^\dagger_\mathbf{p},\left(b^\dagger_\mathbf{p}b^{\vphantom{\dagger}}_\mathbf{p}-1/2\right)\right]=-b^\dagger_\mathbf{p} \end{aligned}

H_\text{pair} is a spin chain H_{\text{pair}}-\mu N=2\sum_\mathbf{p}\xi({\mathbf{p}})S_\mathbf{p}^z+\frac{U_0}{V}\sum_{\mathbf{p},\mathbf{p}'}S^+_\mathbf{p}S^-_{\mathbf{p}'}, where we included chemical potential by defining \xi_\mathbf{p}\equiv\epsilon(\mathbf{p})-\mu.

Parameterize \left(v_\mathbf{p},u_\mathbf{p}\right)=(\cos(\theta_\mathbf{p}/2)e^{i\varphi_\mathbf{p}/2},\sin(\theta_\mathbf{p}/2)e^{-i\varphi_\mathbf{p}/2}) then the variational energy is (except for a constant) \Braket{\text{BCS}|H|\text{BCS}}=\sum_\mathbf{p}\xi_\mathbf{p}\cos\theta_\mathbf{p}+\frac{U_0}{4V}\sum_{\mathbf{p},\mathbf{p}'}\sin \theta_\mathbf{p}\sin\theta_{\mathbf{p}'}\cos\left(\varphi_\mathbf{p}-\varphi_{\mathbf{p}'}\right)
Interpretation
1. First term tends to align spins with z-axis in + direction for \xi_\mathbf{p}<0 and in - direction for \xi_\mathbf{p}>0
2. Second term – from attractive H_\text{int} – wants the spins to lie in the x-y plane

Minimize energy

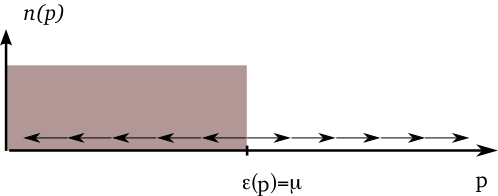
For U_0>0 (repulsive interactions), spins all point in \pm z direction, forming ‘domain wall’ where \xi_{\mathbf{p}} changes sign at Fermi surface
Relationship between spin picture and average number of pairs is \langle n^P_{\mathbf{p}}\rangle=v_\mathbf{p}^2=\left[1+\cos\theta_\mathbf{p}\right]/2, so this corresponds to sharp Fermi step.

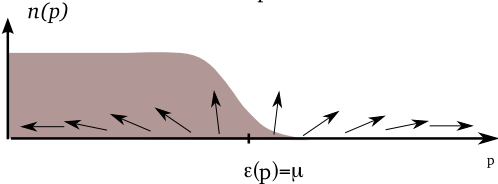
For U_0<0, system can lower its energy by taking \sin\theta_\mathbf{p}\neq 0
Lowering of interaction energy more than compensates increase in kinetic energy that comes from smearing the step
All angles \varphi_\mathbf{p}, describing angle in x-y plane, should be equal

\Braket{\text{BCS}|H|\text{BCS}}=\sum_\mathbf{p}\xi_\mathbf{p}\cos\theta_\mathbf{p}+\frac{U_0}{4V}\sum_{\mathbf{p},\mathbf{p}'}\sin \theta_\mathbf{p}\sin\theta_{\mathbf{p}'} - Taking the extremum of energy with respect to angles \theta_{\mathbf{p}} gives \xi_{\mathbf{p}}\sin\theta_\mathbf{p}+|\Delta|\cos\theta_\mathbf{p}=0, where the gap parameter is \Delta=-\frac{U_0}{2V}\sum_\mathbf{p}e^{i\varphi}\sin\theta_\mathbf{p}=-\frac{U_0}{V}\sum_\mathbf{p}u^*_\mathbf{p}v_\mathbf{p}. \cos\theta_\mathbf{p}=-\frac{\xi_{\mathbf{p}}}{E_\mathbf{p}},\qquad \sin\theta_\mathbf{p}=\frac{|\Delta|}{E_\mathbf{p}}, \qquad E_\mathbf{p}=\sqrt{\xi (\mathbf{p})^2+|\Delta|^2}

Solution corresponds to alignment of spin vector with the direction of the effective `magnetic field’

\left(\mathrm{Re}\,\Delta,\mathrm{Im}\,\Delta,\xi_\mathbf{p}\right)

To be self-consistent, must satisfy the gap equation \Delta=-\frac{U_0}{2V}\sum_\mathbf{p}\frac{\Delta}{E_\mathbf{p}} with continuum limit \Delta=-\frac{U_0}{2}\int \frac{d\mathbf{p}}{\left(2\pi\right)^3} \frac{\Delta}{E_\mathbf{p}}

\Delta=-\frac{U_0}{2}\int \frac{d\mathbf{p}}{\left(2\pi\right)^3} \frac{\Delta}{E_\mathbf{p}}

For U_0>0 there are no non-trivial solutions (\Delta=0 always)
For any U_0<0 there is always a solution at finite \Delta.
Integral divergent at high \mathbf{p}. More significantly, for small \Delta, RHS is \sim-\frac{U_0}{2}\nu(\mu)\Delta\log \Lambda/\Delta, \Lambda is high energy cut-off and \nu(\mu) is density of states per spin
No matter how small the attraction U_0<0, always a solution with finite \Delta. This is the Cooper phenomenon.

Quasiparticle Excitations

Like Bogoliubov, BCS theory also lets us discuss excitations
Can solve BCS hamiltonian by Bogoliubov (we didn’t) but can introduce Bogoliubov-type excitations after the fact

\lvert{\text{BCS}}\rangle =\prod_\mathbf{p}\left[v_\mathbf{p}a^\dagger_{\mathbf{p}\uparrow}a^\dagger_{-\mathbf{p}\downarrow}+u_\mathbf{p}\right]\lvert{\text{VAC}}\rangle

Can show that \begin{align*} \alpha^{\vphantom{\dagger}}_{\mathbf{p}\uparrow}&=u_{\mathbf{p}}a^{\vphantom{\dagger}}_{\mathbf{p}\uparrow}-v_{\mathbf{p}}a^\dagger_{-\mathbf{p}\downarrow}\\ \alpha^{\vphantom{\dagger}}_{\mathbf{p}\downarrow}&=u_{-\mathbf{p}}a^{\vphantom{\dagger}}_{\mathbf{p}\downarrow}+v_{-\mathbf{p}}a^\dagger_{-\mathbf{p}\uparrow}, \end{align*} satisfy fermion anticommutation relations and annihilate BCS state \alpha^{\vphantom{\dagger}}_{\mathbf{p},s}\lvert{\text{BCS}}\rangle=0.

\lvert{\mathbf{p},s}\rangle=\alpha^\dagger_{\mathbf{p},s}\lvert{\text{BCS}}\rangle=a^\dagger_{\mathbf{p},s}\prod_{\mathbf{p}'\neq \mathbf{p}} \left[v_{\mathbf{p}'}a^\dagger_ {\mathbf{p}'\uparrow}a^\dagger_{-\mathbf{p}'\downarrow}+u_{\mathbf{p}'}\right]\lvert{\text{VAC}}\rangle,

If we chose s=\uparrow so that \left(\mathbf{p},\uparrow\right) state is certainly occupied it means that a^\dagger_{\mathbf{p} \uparrow}a^\dagger_{-\mathbf{p}\downarrow}\lvert{\mathbf{p},\uparrow}\rangle=0
Corresponding term no longer appears in interaction term when it is applied to this state
The level is said to be `blocked’. Thus it certainly is an eigenstate of the pair problem, if \lvert{\text{BCS}}\rangle is. What is its energy?

Have to take into account kinetic energy as well as loss of attractive interaction energy

E_{s}(\mathbf{p})=\xi_{\mathbf{p}}[\overbrace{\left(1-\langle n^P_\mathbf{p}\rangle\right)}^{\left(\mathbf{p},s\right)\,\mathrm{occupied}} \overbrace{-\langle n^P_\mathbf{p}\rangle}^{\left(-\mathbf{p},-s\right)\,\mathrm{empty}}]+\overbrace{\Delta\sin\theta_ \mathbf{p}}^{\mathrm{`blocking'}}=E_{\mathbf{p}}

These quasiparticle excitations always have a gap \Delta_{s} given by

\Delta_s=\min_\mathbf{p}E_\mathbf{p}=\begin{cases} \Delta, & \mu>0,\\ \sqrt{\Delta^2+\mu^2},& \mu<0. \end{cases}

Features of the quasiparticle dispersion