Second Quantization

Avoid dealing explicitly with \Psi(\mathbf{r}_1,\ldots,\mathbf{r}_N)
Represent H and other operators using occupation numbers
Synonymous with Quantum Field Theory

Recap: Product States

Normalized state of N bosons in orthonormal states \varphi_{\alpha_n}(\mathbf{r})

\Psi^{\text{S}}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}(\mathbf{r}_1,\ldots,\mathbf{r}_N)=\sqrt{\frac{\prod_{\alpha}N_{\alpha}!}{N!}}\sum_P\varphi_{\alpha_{1}}(\mathbf{r}_{P_1})\varphi_{\alpha_{2}}(\mathbf{r}_{P_2})\cdots\varphi_{\alpha_{N}}(\mathbf{r}_{P_N})

The normalization factor involves occupation numbers \{N_{\alpha}\} giving number of particles in state \alpha

Unnormalized symmetric product state using \psi_n(\mathbf{r}), not necessarily orthonormal

\Psi^{\text{S}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) = \frac{1}{\sqrt{N!}}\sum_P\psi_1(\mathbf{r}_{P_1})\psi_{2}(\mathbf{r}_{P_2})\cdots\psi_{N}(\mathbf{r}_{P_N})

Inner product with another symmetric state formed from \phi_n(\mathbf{r})

\Phi^{\text{S}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) = \frac{1}{\sqrt{N!}}\sum_P\phi_1(\mathbf{r}_{P_1})\phi_{2}(\mathbf{r}_{P_2})\cdots\phi_{N}(\mathbf{r}_{P_N})

\langle{\Psi}\rvert\Phi\rangle = \sum_P \prod_{n=1}^N\langle{\psi_n}\rvert\phi_{P_n}\rangle = \operatorname{perm} \langle{\psi_m}\rvert\phi_{n}\rangle

This is the permanent of the matrix \langle{\psi_m}\rvert\phi_{n}\rangle

Goal

For SHO

\frac{1}{\sqrt{n!}}\left(a^\dagger\right)^n\lvert{0}\rangle\longleftrightarrow \psi_n(x) representation using a^{\vphantom{\dagger}}, a^\dagger very useful; never need explicit \psi_n(x)

We want

??\longleftrightarrow \Psi^{\text{S}}(\mathbf{r}_1,\ldots,\mathbf{r}_N)

Must respect inner product

Creation & Annihilation Operators

We consider states with different numbers of particles
\lvert{\text{VAC}}\rangle denotes state with no particles (the vacuum state)
a^\dagger(\psi) creates particle in single particle state \psi(\mathbf{r})

\psi(\mathbf{r})\longleftrightarrow a^\dagger(\psi)\lvert{\text{VAC}}\rangle

Evidently, a^\dagger(\psi) must be linear in \psi

a^\dagger\left(c_1\psi_1+c_2\psi_2\right) = c_1a^\dagger(\psi_1)+c_2a^\dagger(\psi_2)

If \lvert{\Psi}\rangle has N particle state, a^\dagger(\psi)\lvert{\Psi}\rangle has N+1 particles
Since this is orthogonal to the vacuum state

\langle{\text{VAC}}\rvert a^\dagger(\psi)\lvert{\Psi}\rangle=0 for any state \lvert{\Psi}\rangle

Taking the adjoint, this means

a^{\vphantom{\dagger}}(\psi)\lvert{\text{VAC}}\rangle=0

N particle product state

\Psi^{\text{S}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) \longleftrightarrow a^\dagger(\psi_1)\cdots a^\dagger(\psi_N)\lvert{\text{VAC}}\rangle

To be symmetric wavefunction, we must have

\left[a^\dagger(\psi),a^\dagger(\phi)\right]=0 for any states \psi(\mathbf{r}) and \phi(\mathbf{r}). Taking the adjoint gives

\left[a^{\vphantom{\dagger}}(\psi),a^{\vphantom{\dagger}}(\phi)\right]=0

Inner product between two one particle states

\langle{\psi}\rvert\phi\rangle = \langle{\text{VAC}}\rvert a^{\vphantom{\dagger}}(\psi)a^\dagger(\phi) \lvert \text{VAC} \rangle

We impose

\left[a^{\vphantom{\dagger}}(\psi),a^\dagger(\phi)\right] = \langle{\psi}\rvert \phi \rangle together with a^{\vphantom{\dagger}}(\psi)\lvert{\text{VAC}}\rangle=0 this gives correct inner product

Check

Show that this also reproduces the inner product for N-particle product states

Choosing a basis

Orthonormal basis by \varphi_\alpha(\mathbf{r})

a^\dagger(\varphi_\alpha)\equiv a^\dagger_\alpha,\quad a^{\vphantom{\dagger}}(\varphi_\alpha)\equiv a^{\vphantom{\dagger}}_\alpha

Then we have

\begin{aligned} \left[a^{\vphantom{\dagger}}_\alpha,a^{\vphantom{\dagger}}_\beta\right]=0,\quad \left[a^\dagger_\alpha,a^\dagger_\beta\right]=0,\quad \left[a^{\vphantom{\dagger}}_\alpha,a^\dagger_\beta\right] = \delta_{\alpha\beta} \end{aligned}

Same as ladder operators of a set of harmonic oscillators

\Psi^{\text{S}}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) \longleftrightarrow\lvert{\mathbf{N}}\rangle \equiv \prod_\alpha \frac{\left(a^\dagger_\alpha\right)^{N_\alpha}}{\sqrt{N_\alpha!}}\lvert{\text{VAC}}\rangle

\mathsf{N}^{\vphantom{\dagger}}_{\alpha}\equiv a^\dagger_{\alpha}a^{\vphantom{\dagger}}_{\alpha} is number operator for state \alpha

\mathsf{N}^{\vphantom{\dagger}}_{\alpha}\lvert{\mathbf{N}}\rangle=N_{\alpha}\lvert{\mathbf{N}}\rangle

Commutation relations tell us

\begin{aligned} \left[a^{\vphantom{\dagger}}_{\alpha},\mathsf{N}^{\vphantom{\dagger}}_{\alpha}\right]=a^{\vphantom{\dagger}}_{\alpha}\qquad \left[a^\dagger_{\alpha},\mathsf{N}^{\vphantom{\dagger}}_{\alpha}\right]=-a^\dagger_{\alpha} \end{aligned}

I think of the first one as:

“count then destroy minus destroy then count”

Change of basis

Move to different basis \{\lvert{\tilde{\varphi}_{\alpha}}\rangle\}

\lvert{\tilde{\varphi}_{\alpha}}\rangle=\sum_{\beta} \langle{\varphi_{\beta}}\rvert \tilde{\varphi}_{\alpha} \rangle\lvert{\varphi_{\beta}}\rangle

One particle states with wavefunctions \varphi_{\alpha}(\mathbf{r}) are a^\dagger_{\alpha}\lvert{\text{VAC}}\rangle. So,

\tilde{a^{\vphantom{\dagger}}}_{\alpha}^\dagger\equiv\sum_{\beta} \langle{\varphi_{\beta}}\rvert \tilde{\varphi}_{\alpha} \rangle a^\dagger_{\beta}

Often we work in position eigenstates \{\lvert{\mathbf{r}}\rangle\}, so \langle{\varphi_{\beta}}\rvert \mathbf{r} \rangle=\varphi^{*}_{\beta}(\mathbf{r})
Denoting corresponding creation operator as \psi^\dagger(\mathbf{r})

\psi^\dagger(\mathbf{r})\equiv\sum_{\beta} \varphi^{*}_{\beta}(\mathbf{r})a^\dagger_{\beta}

Conjugate is

\psi^{\vphantom{\dagger}}(\mathbf{r})\equiv\sum_{\beta} \varphi_{\beta}(\mathbf{r})a^{\vphantom{\dagger}}_{\beta}

These are quantum fields with commutation relations

\begin{gather*} \left[\psi^{\vphantom{\dagger}}(\mathbf{r}_1),\psi^\dagger(\mathbf{r}_2)\right]=\delta(\mathbf{r}_1-\mathbf{r}_2)\nonumber\\ \left[\psi^{\vphantom{\dagger}}(\mathbf{r}_1),\psi^{\vphantom{\dagger}}(\mathbf{r}_2)\right]=\left[\psi^\dagger(\mathbf{r}_1),\psi^\dagger(\mathbf{r}_2)\right]=0 \end{gather*}

Check

If a state \lvert{\Psi}\rangle has wavefunction \Psi(x_1,\ldots, x_N), show that the wavefunction of the state \psi^{\vphantom{\dagger}}(X)\lvert{\Psi}\rangle is the N-1 particle wavefunction

\sqrt{N}\Psi(X,x_1,\ldots, x_{N-1})

Hint: Show that is is true for a product state first.

Often use eigenstates of the free particle Hamiltonian H=\frac{\mathbf{p}^{2}}{2m}

\begin{aligned} \lvert{\mathbf{k}}\rangle=\frac{\exp(i\mathbf{k}\cdot \mathbf{r})}{\sqrt{V}}, \quad \mathbf{k}=2\pi\left(\frac{n_{x}}{L_{x}},\frac{n_{y}}{L_{y}},\frac{n_{z}}{L_{z}}\right),\quad n_{x,y,z}\text{ integer}, \end{aligned} with V=L_{x}L_{y}L_{z} (periodic b.c.)

Matrix elements of transformation between to position basis \{\lvert{\mathbf{r}}\rangle\} are \langle{\mathbf{k}}\rvert\mathbf{r}\rangle=\exp(-i\mathbf{k}\cdot \mathbf{r})/\sqrt{V} \psi^\dagger(\mathbf{r})\equiv\frac{1}{\sqrt{V}}\sum_{\mathbf{k}} \exp(-i\mathbf{k}\cdot\mathbf{r})a^\dagger_{\mathbf{k}} and similarly \psi^{\vphantom{\dagger}}(\mathbf{r})\equiv\frac{1}{\sqrt{V}}\sum_{\mathbf{k}} \exp(i\mathbf{k}\cdot\mathbf{r})a^{\vphantom{\dagger}}_{\mathbf{k}}

Check

What is the wavefunction of the two-particle state

\sum_\mathbf{k}c_\mathbf{k}a^\dagger_\mathbf{k}a^\dagger_{-\mathbf{k}}\lvert{\text{VAC}}\rangle?

Fermions

Trickier on account of minus signs! Seek a representation of

\Psi^{\text{A}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) = \frac{1}{\sqrt{N!}}\sum_P (-1)^P\psi_1(\mathbf{r}_{P_1})\psi_{2}(\mathbf{r}_{P_2})\cdots\psi_{N}(\mathbf{r}_{P_N})

Note: overall sign fixed by labelling of states \psi_j

If \Psi^{\text{A}}(\mathbf{r}_1,\ldots,\mathbf{r}_N) \longleftrightarrow a^\dagger(\psi_1)\cdots a^\dagger(\psi_N)\lvert{\text{VAC}}\rangle we’ll need

\left\{a^\dagger(\psi),a^\dagger(\phi)\right\}=0, \{A,B\}\equiv AB+BA is anticommutator. Also

\left\{a^{\vphantom{\dagger}}(\psi),a^{\vphantom{\dagger}}(\phi)\right\}=0

\left\{a^{\vphantom{\dagger}}(\psi),a^\dagger(\phi)\right\}=0` can be deduced from inner product

\langle{\Psi}\rvert\Phi\rangle = \sum_P (-1)^P\prod_{n=1}^N\langle{\psi_n}\rvert\phi_{P_n}\rangle = \det \langle{\psi_m}\rvert\phi_{n}\rangle,

which works out if

\left\{a^{\vphantom{\dagger}}(\psi),a^\dagger(\phi)\right\} = \langle{\psi}\rvert \phi \rangle

Check

Check this.

Introducing field operators in position basis as before leads to

\begin{gather*} \left\{\psi^{\vphantom{\dagger}}(\mathbf{r}_1),\psi^\dagger(\mathbf{r}_2)\right\}=\delta(\mathbf{r}_1-\mathbf{r}_2)\nonumber\\ \left\{\psi^{\vphantom{\dagger}}(\mathbf{r}_1),\psi^{\vphantom{\dagger}}(\mathbf{r}_2)\right\}=\left\{\psi^\dagger(\mathbf{r}_1),\psi^\dagger(\mathbf{r}_2)\right\}=0 \end{gather*}

Explicit Form of Operators

Check

Think about the form that the operators a^{\vphantom{\dagger}}_\alpha, a^\dagger_\alpha take in the basis of product states. Start with one state \varphi_\alpha. What’s the matrix form of a^\dagger_\alpha in terms of states \lvert{N_\alpha}\rangle? Now consider two states. Can you see how the commutation and anticommutation relations can be satisfied?

Single Particle Operators

Notation: A acts on single particle states; \hat A acts on N particles as

\hat A = \sum_{j=1}^N A_j

Example: Hamiltonian for noninteracting particles

\hat H = \sum_{j=1}^N H_j = \sum_{j=1}^N \left[-\frac{\nabla_j^2}{2m}+V(\mathbf{r}_j)\right]

Operators of this type are single particle operators
How to represent them using creation and annihilation operators?

Action of A on states \lvert{\varphi_\alpha}\rangle written

A\lvert{\varphi_\alpha}\rangle = \sum_{\beta} \lvert{\varphi_\beta}\rangle\langle{\varphi_\beta}\rvert A \lvert \varphi_\alpha \rangle = \sum_\beta A_{\beta\alpha}\lvert{\varphi_\beta}\rangle

Action of \hat A on product state \lvert{\Psi^{\text{S/A}}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle is

\hat A \lvert{\Psi^{\text{S/A}}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle = \sum_\beta \left[A_{\beta\alpha_1}\lvert{\Psi^{\text{S/A}}_{\beta\alpha_{2}\cdots\alpha_{N}}}\rangle +A_{\beta\alpha_2}\lvert{\Psi^{\text{S/A}}_{\alpha_1\beta\cdots\alpha_{N}}}\rangle+\cdots A_{\beta\alpha_N}\lvert{\Psi^{\text{S/A}}_{\alpha_1\alpha_{2}\cdots\beta}}\rangle\right]

We’ll see same job is done by

\hat A = \sum_{\alpha\beta}A_{\alpha\beta}a^\dagger_\alpha a^{\vphantom{\dagger}}_\beta acting on state \lvert{\mathbf{N}}\rangle \equiv \prod_\alpha \frac{\left(a^\dagger_\alpha\right)^{N_\alpha}}{\sqrt{N_\alpha!}}\lvert{\text{VAC}}\rangle

We have

\left[a^\dagger_\alpha a^{\vphantom{\dagger}}_\beta,a^\dagger_\gamma\right]=a^\dagger_\alpha\delta_{\beta\gamma} for bosons and fermions

Commute a^\dagger_\alpha a^{\vphantom{\dagger}}_\beta though each of creation operators in \lvert{\mathbf{N}}\rangle, e.g.

\begin{aligned} \mathop{\hat A}a^\dagger_{\beta}\lvert{\text{VAC}}\rangle&=\left(\left[\mathop{\hat A},a^\dagger_{\beta}\right]+a^\dagger_{\beta}\mathop{\hat A}\right)\lvert{\text{VAC}}\rangle\nonumber\\ &=\sum_{\alpha} A_{\alpha \beta} a^\dagger_{\alpha}\lvert{\text{VAC}}\rangle \end{aligned}

Check

Try it for a two particle state!

\hat A = \sum_{\alpha\beta}A_{\alpha\beta}a^\dagger_\alpha a^{\vphantom{\dagger}}_\beta

Find matrix element \langle{\mathbf{N}}\rvert \hat A \lvert \mathbf{N'} \rangle between product states made of orthonormal single particle states
Vanishes unless N_\beta = N'_\beta-1 and N_\alpha = N'_\alpha+1 we have

\langle{\mathbf{N}}\rvert \hat A \lvert \mathbf{N'} \rangle = A_{\alpha\beta} \sqrt{N_\alpha N'_\beta}

Check

This formula is not so easy to work out in the first quantized representation. Try it!

Same for bosons and fermions

\hat A = \sum_{\alpha\beta}A_{\alpha\beta}a^\dagger_\alpha a^{\vphantom{\dagger}}_\beta

Like expectation value of \mathop{A} in single particle state \sum_{\alpha}a_{\alpha}\lvert{\varphi_{\alpha}}\rangle
But a_\alpha are operators not numbers. This is the origin of the name second quantization
Resemblance makes it easy to write down second quantized form

Example 1: noninteracting Hamiltonian

\hat H = \sum_{j=1}^N H_j = \sum_{j=1}^N \left[-\frac{\nabla_j^2}{2m}+V(\mathbf{r}_j)\right]

Second quantized form \mathop{\hat H} \equiv \sum_{\alpha,\beta}\langle{\varphi_{\alpha}}\rvert \mathop{H} \lvert \varphi_{\beta} \rangle a^\dagger_{\alpha}a^{\vphantom{\dagger}}_{\beta}, H is single particle Hamiltonian H=-\frac{1}{2m}\nabla_{i}^{2}+V(\mathbf{r_{i}})
If basis \lvert{\varphi_{\alpha}}\rangle is eigenbasis of H: \langle{\varphi_{\alpha}}\rvert \mathop{H} \lvert \varphi_{\beta} \rangle=E_{\alpha}\delta_{\alpha \beta} and

\begin{aligned} \mathop{\hat H} \equiv \sum_{\alpha} E_{\alpha} a^\dagger_{\alpha}a^{\vphantom{\dagger}}_{\alpha}=\sum_{\alpha} E_{\alpha} \mathsf{N}^{\vphantom{\dagger}}_{\alpha} \end{aligned}

In the position basis

\begin{aligned} \mathop{\hat H}&=\int d\mathbf{r}\left[-\frac{1}{2m}\psi^\dagger(\mathbf{r})\nabla^{2}\psi^{\vphantom{\dagger}}(\mathbf{r})+V(\mathbf{r})\psi^\dagger(\mathbf{r})\psi^{\vphantom{\dagger}}(\mathbf{r})\right]\nonumber\\ &=\int d\mathbf{r}\left[\frac{1}{2m}\nabla\psi^\dagger(\mathbf{r})\cdot\nabla\psi^{\vphantom{\dagger}}(\mathbf{r})+V(\mathbf{r})\psi^\dagger(\mathbf{r})\psi^{\vphantom{\dagger}}(\mathbf{r})\right], \end{aligned} (integration by parts)

Confirm equality to previous expression using

\psi^{\vphantom{\dagger}}(\mathbf{r})\equiv\sum_{\beta} \varphi_{\beta}(\mathbf{r})a^{\vphantom{\dagger}}_{\beta}

Heisenberg equation of motion for \psi^{\vphantom{\dagger}}(\mathbf{r})=e^{i\hat Ht}\psi^{\vphantom{\dagger}}(\mathbf{r}) e^{-i\hat H t} with noninteracting Hamiltonian

\begin{split} i\partial_{t}\psi^{\vphantom{\dagger}}(\mathbf{r},t) &= -\left[\mathop{\hat H},\psi^{\vphantom{\dagger}}(\mathbf{r},t)\right]\\ &= -\frac{1}{2m}\nabla^{2}\psi^{\vphantom{\dagger}}(\mathbf{r},t)+V(\mathbf{r})\psi^{\vphantom{\dagger}}(\mathbf{r},t) \end{split} just the time dependent Schrödinger equation!

Example 2: Density

Single particle operator for density at \mathbf{x} is

\rho(\mathbf{x})\equiv\delta(\mathbf{x}-\mathbf{r})

Expectation value in single particle state \varphi(\mathbf{r}) is \rho(\mathbf{x})=\lvert{\varphi(\mathbf{x})}\rvert^{2}
Second quantized form of the operator is then

\hat\rho(\mathbf{x})\equiv\psi^\dagger(\mathbf{x})\psi^{\vphantom{\dagger}}(\mathbf{x})

Check: integrating over position should give total number of particles

\hat N=\int d\mathbf{x}\, \psi^\dagger(\mathbf{x})\psi^{\vphantom{\dagger}}(\mathbf{x})=\sum_{\alpha} a^\dagger_{\alpha}a^{\vphantom{\dagger}}_{a}=\sum_{\alpha}\mathsf{N}^{\vphantom{\dagger}}_{\alpha}

Expectation value of density in product state \lvert{N_{0},N_{1}\ldots}\rangle

\langle{N_{0},N_{1}\ldots}\rvert \hat\rho(\mathbf{r}) \lvert N_{0},N_{1}\ldots \rangle = \sum_{\alpha} N_{\alpha}\left|\varphi_{\alpha}(\mathbf{r})\right|^{2}.

Check

Prove using \psi^{\vphantom{\dagger}}(\mathbf{r})\equiv\sum_{\beta} \varphi_{\beta}(\mathbf{r})a^{\vphantom{\dagger}}_{\beta}

Interpretation: \left|\varphi_{\alpha}(\mathbf{r})\right|^{2} is probability to find a particle in state \alpha at position \mathbf{r}. Density is weighted by occupation

Example 3: Current operator

\hat{\mathbf{j}}(\mathbf{r})=-i\frac{1}{2m}\left[\psi^\dagger(\mathbf{r})\left(\nabla\psi^{\vphantom{\dagger}}(\mathbf{r})\right)-\left(\nabla\psi^\dagger(\mathbf{r})\right)\psi^{\vphantom{\dagger}}(\mathbf{r})\right].

Often we consider Fourier components of density or current

\begin{aligned} \hat\rho_{\mathbf{q}}\equiv\int d\mathbf{r}\, \hat\rho(\mathbf{r})e^{-i\mathbf{q}\cdot \mathbf{r}}=\sum_{\mathbf{k}} a^\dagger_{\mathbf{k}-\mathbf{q}/2}a^{\vphantom{\dagger}}_{\mathbf{k}+\mathbf{q}/2}\nonumber\\ \hat{\mathbf{j}}_{\mathbf{q}}\equiv\int d\mathbf{r}\, \hat{\mathbf{j}}(\mathbf{r})e^{-i\mathbf{q}\cdot \mathbf{r}}=\sum_{\mathbf{k}} \frac{\mathbf{k}}{m}a^\dagger_{\mathbf{k}-\mathbf{q}/2}a^{\vphantom{\dagger}}_{\mathbf{k}+\mathbf{q}/2}. \end{aligned}

\mathbf{q}=0 modes are total particle number and \frac{1}{m}\times total momentum, respectively

Single particle density matrix

From Lecture 1

g(\mathbf{r},\mathbf{r}') \equiv N \int d\mathbf{r}_{2}\cdots d\mathbf{r}_{N}\,\Psi^{*}(\mathbf{r},\mathbf{r}_{2},\ldots,\mathbf{r}_{N})\Psi(\mathbf{r}',\mathbf{r}_{2},\ldots,\mathbf{r}_{N}).

Check

Show that this can be written as

g(\mathbf{r},\mathbf{r}')= \langle{\Psi}\rvert \psi^\dagger(\mathbf{r})\psi^{\vphantom{\dagger}}(\mathbf{r}') \lvert \Psi \rangle

Similar calculation as for density gives

g(\mathbf{r},\mathbf{r}') = \sum_{\alpha} N_{\alpha}\varphi_{\alpha}^{*}(\mathbf{r})\varphi^{}_{\alpha}(\mathbf{r}')

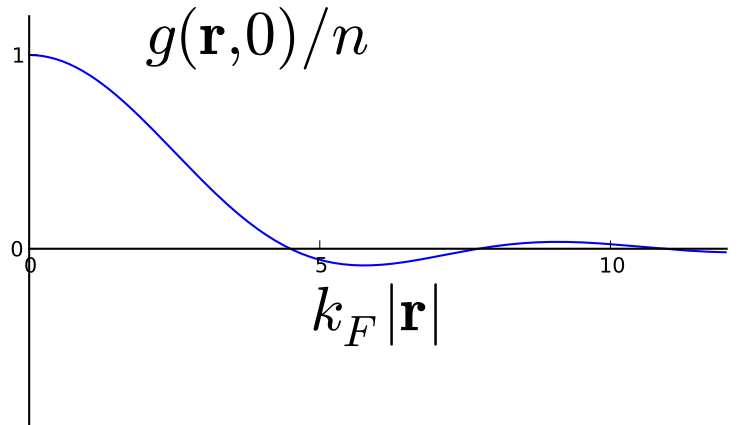
For 3D N_{\mathbf{k}}=1 for \lvert{\mathbf{k}}\rvert<k_{F}, and 0 otherwise

\lvert{\text{Fermi sea}}\rangle = \prod_{|\mathbf{k}|<k_F} a^\dagger_\mathbf{k}\lvert{\text{VAC}}\rangle

Check

\begin{aligned} g(\mathbf{r},\mathbf{r}')&=\frac{1}{V}\sum_{|\mathbf{k}|<k_{F}} e^{i\mathbf{k}\cdot(\mathbf{r}'-\mathbf{r})}=\int_{|\mathbf{k}|<k_{F}} \frac{d\mathbf{k}}{(2\pi)^{3}}\,e^{i\mathbf{k}\cdot(\mathbf{r}'-\mathbf{r})}\nonumber\\ &=\frac{k_{F}^{3}}{2\pi^{2}}\left[\frac{\sin\left(k_{F}|\mathbf{r}'-\mathbf{r}|\right)}{(k_{F}|\mathbf{r}'-\mathbf{r}|)^{3}}-\frac{\cos\left(k_{F}|\mathbf{r}'-\mathbf{r}|\right)}{(k_{F}|\mathbf{r}'-\mathbf{r}|)^{2}}\right]. \end{aligned}

Note that g(\mathbf{r},\mathbf{r})=\frac{k_{F}^{3}}{6\pi^{2}}=n

c.f. earlier calculation in 1D using Slater determinant

Two Particle Operators

Acts pairwise on the particles (B_{jk}=B_{kj} for indistinguishable particles.)

\hat B = \sum_{j<k} B_{jk}.

Action of \hat B on product state \lvert{\varphi_{\alpha}}\rangle_1\lvert{\varphi_{\beta}}\rangle_2 in terms of matrix elements

\begin{aligned} B_{\alpha\beta,\gamma\delta} &= \langle{\varphi_\alpha}\rvert_1\langle{\varphi_\beta}\rvert_2 B_{12} \lvert{\varphi_\gamma}\rangle_1\lvert{\varphi_\delta}\rangle_2\\ \hat B &= \frac{1}{2}\sum_{\alpha\beta\gamma\delta} B_{\alpha\beta,\gamma\delta}a^\dagger_\alpha a^\dagger_\beta a^{\vphantom{\dagger}}_\delta a^{\vphantom{\dagger}}_\gamma,\qquad B_{\alpha\beta,\gamma\delta} = B_{\beta\alpha,\delta\gamma} \end{aligned} (Note order, which is important for fermions!)

Check

Check this works on product states (N=2 first)

Remember that for one particle operators

\langle{\mathbf{N}}\rvert \hat A \lvert \mathbf{N'} \rangle = A_{\alpha\beta} \sqrt{N_\alpha N'_\beta}

For two particle operators

\langle{\mathbf{N}}\rvert \hat B \lvert \mathbf{N'} \rangle = \left[B_{\alpha\beta,\gamma\delta}\pm B_{\alpha\beta,\delta\gamma}\right] \sqrt{N_\alpha N_\beta N'_\gamma N'_\delta} with N_{\gamma,\delta} = N'_{\gamma,\delta}-1 and N_{\alpha,\beta} = N'_{\alpha,\beta}+1

For fermions the overall sign depends on convention: best to write states explicitly rather than matrix elements

\langle{\mathbf{N}}\rvert \hat B \lvert \mathbf{N'} \rangle = \left[B_{\alpha\beta,\gamma\delta}\pm B_{\alpha\beta,\delta\gamma}\right] \sqrt{N_\alpha N_\beta N'_\gamma N'_\delta}.

Strictly we have

\begin{gather*} N'_\gamma N'_\delta \to N'_\gamma (N'_\gamma-1) && \gamma=\delta\\ N_\alpha N_\beta \to N_\alpha (N_\alpha-1) && \alpha=\beta \end{gather*} In thermodynamic limit these terms usually make a vanishing contribution when sums replaced with integrals

Exceptions: when a finite fraction of particles are in one state (which occurs for Bose—Einstein condensates). In those cases we end up neglecting N_\alpha-1 relative to N_\alpha, however!

Example: pairwise interaction

\hat H_\text{int.} = \sum_{j<k} U(\mathbf{r}_j-\mathbf{r}_k).

Expressing in position basis

\hat H_\text{int.} = \frac{1}{2}\int d\mathbf{r}_1 d\mathbf{r}_2\, U(\mathbf{r}_1-\mathbf{r}_2)\psi^\dagger(\mathbf{r}_1)\psi^\dagger(\mathbf{r}_2)\psi^{\vphantom{\dagger}}(\mathbf{r}_2)\psi^{\vphantom{\dagger}}(\mathbf{r}_1)

Remembering that \rho(\mathbf{r}) = \psi^\dagger(\mathbf{r})\psi^{\vphantom{\dagger}}(\mathbf{r}), this is almost

\frac{1}{2}\int d\mathbf{r}_1 d\mathbf{r}_2\, U(\mathbf{r}_1-\mathbf{r}_2)\rho(\mathbf{r}_1)\rho(\mathbf{r}_2) Operator order prevents a particle from interacting with itself!

Check

\hat H_\text{int} has zero expectation for 1 particle

Hamiltonian of interacting bosons from Lecture 1

H = -\frac{1}{2m}\sum_j \frac{\partial^2}{\partial x_j^2} + \overbrace{c\sum_{j<k}\delta(x_j-x_k)}^{\equiv H_\text{int}}. has second quantized form H = \int dx \left[\frac{1}{2}\partial_x\psi^\dagger(x)\partial_x\psi^{\vphantom{\dagger}}(x) + \frac{c}{2}\psi^\dagger(x)\psi^\dagger(x)\psi^{\vphantom{\dagger}}(x)\psi^{\vphantom{\dagger}}(x)\right] \psi^{\vphantom{\dagger}}(x), \psi^\dagger(x) satisfy the canonical bosonic commutation relations

QFT is a language, but writing something in a new way doesn’t (necessarily) make it easier to solve!