Response and Correlation
Response & Correlation
Calculating eigenstates and eigenenergies is one thing, but what do experimentalists actually measure?
Want to understand how many body systems respond dynamically to an external probe
Time evolution of spontaneous fluctuations (thermal or quantum) obeys similar dynamics \longrightarrow fluctuation–dissipation relation
Quantum fluctuations: one oscillator
- For a single (undamped) oscillator we have ground state fluctuations H = \frac{p^2}{2m} + \frac{1}{2}m\omega_0^2 y^2 \langle{0}\rvert y^2 \lvert{0}\rangle = \frac{1}{2m \omega_0}
At finite temperature \langle\langle y^2\rangle\rangle=\mathop{\mathrm{tr}}\left[\rho\\, y^2\right] = \frac{\coth(\beta\omega_0/2)}{2m\omega_0} \rho = e^{-\beta H}/Z is equilibrium density matrix, and Z=\mathop{\mathrm{tr}}[e^{-\beta H}] is partition function
The double angular brackets \langle\langle (\cdots)\rangle\rangle denote that we are taking quantum and thermal expectations.
What about time dependent fluctuations? A natural candidate: \langle\langle y(t)y(0)\rangle\rangle, y(t) = e^{iHt} y e^{-iHt} (Heisenberg picture)
This gives the quantum noise spectrum
S(\omega) = \int_{-\infty}^\infty \langle\langle y(t)y(0)\rangle\rangle e^{i\omega t}\,dt.
- BUT: since y(0) and y(t) do not commute with each other \langle\langle y(t)y(0)\rangle\rangle\neq \langle\langle y(0)y(t)\rangle\rangle=\langle\langle y(-t)y(0)\rangle\rangle, so
S(\omega)\neq S(-\omega)
Many of the properties of S(\omega) are most easily understood from spectral representation
Insert complete set of energy eigenstates between y(0) and y(t)
S(\omega) = 2\pi\sum_{m,n} \frac{e^{-\beta E_n}}{Z} |\langle{n}\rvert y\lvert{m}\rangle|^2 \delta(\omega-E_m+E_n)
- Reason for asymmetry in S(\omega) is that term with \delta(\omega-E_m+E_n) is weighted by e^{-\beta E_n}, while term with \delta(\omega-E_n+E_m) has e^{-\beta E_m}
S(\omega) = S(-\omega) e^{\beta\omega}.
At zero temperature \beta\to\infty and we can see that S(\omega<0)=0.
Let’s evaluate S(\omega) for oscillator. The matrix elements are \langle{n}\rvert y\lvert{m}\rangle = \frac{1}{\sqrt{2m\omega_0}}\begin{cases} \sqrt{m+1} & \text{if } n=m+1 \\ \sqrt{m} & \text{if } n=m-1. \end{cases} \begin{align*} S(\omega)&=\frac{\pi}{m\omega_0} \sum_n \frac{e^{-\beta E_n}}{Z} \left[n\delta(\omega+\omega_0)+(n+1)\delta(\omega-\omega_0)\right]\nonumber\\ & = \frac{\pi}{m\omega_0}\left[n_\text{B}(\omega_0)\delta(\omega+\omega_0)+(n_\text{B}(\omega_0)+1)\delta(\omega-\omega_0)\right] \end{align*} n_\text{B}(\omega)\equiv \frac{1}{\exp\left(\beta\omega\right)-1} is Bose distribution function
\begin{align*} S(\omega)&=\frac{\pi}{m\omega_0} \sum_n \frac{e^{-\beta E_n}}{Z} \left[n\delta(\omega+\omega_0)+(n+1)\delta(\omega-\omega_0)\right]\nonumber\\ & = \frac{\pi}{m\omega_0}\left[n_\text{B}(\omega_0)\delta(\omega+\omega_0)+(n_\text{B}(\omega_0)+1)\delta(\omega-\omega_0)\right] \end{align*}
- Shows the predicted asymmetry between positive and negative frequencies. We can check that \int S(\omega)\frac{d\omega}{2\pi} = \langle\langle y^2\rangle\rangle= \frac{\coth(\beta\omega_0/2)}{2m\omega_0} as we found before.
Classical limit \beta\omega\to 0
\begin{align*} S(\omega)&= \frac{\pi}{m\omega_0}\left[n_\text{B}(\omega_0)\delta(\omega+\omega_0)+(n_\text{B}(\omega_0)+1)\delta(\omega-\omega_0)\right]\\\\ &\to \frac{k_\text{B}T}{2m\omega_0^2} \times 2\pi\left[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)\right] \end{align*}
- Consistent with equipartition: \frac{1}{2}m\omega_0^2 \langle y^2\rangle=\frac{1}{2}k_\text{B}T
Many oscillators
- We can express y(t) in terms of normal modes as y(t) = \sum_k \left[c^{}_k a^\dagger_k(t) + c_k^* a^{\vphantom{\dagger}}_k(t)\right]
- Time evolution of mode operators is
a^\dagger_k(t) = e^{i\omega_k t}a^\dagger_k,\quad a^{\vphantom{\dagger}}_k(t) = e^{-i\omega_k t}a^{\vphantom{\dagger}}_k
- Repeating calculation of S(\omega) gives
\begin{align*} S(\omega)= 2\pi\sum_k |c_k|^2\left[n_\text{B}(\omega_k)\delta(\omega+\omega_k)+(n_\text{B}(\omega_k)+1)\delta(\omega-\omega_k)\right] \end{align*}
- In continuum limit sum of \delta(\omega\pm\omega_k)\longrightarrow smooth S(\omega)
Response of oscillator system
Solve Heisenberg equations of motion H = \sum_k \omega_k a^\dagger_ka^{\vphantom{\dagger}}_k - f(t)y, where y is written in terms of normal modes \frac{da^{\vphantom{\dagger}}_k}{dt} = -i\omega_k a^{\vphantom{\dagger}}_k +i c_k f(t),
Solution is a^{\vphantom{\dagger}}_k(t) = e^{-i\omega_k t}a^{\vphantom{\dagger}}_k(0)+a_{k,f}(t) with a^{\vphantom{\dagger}}_{k,f}(\omega) \equiv \frac{c_k}{\omega_k-\omega-i0} f(\omega). (-i0 introduced for response analytic in UHP i.e. causal)
- Response of a^{\vphantom{\dagger}}_k(t)\longrightarrow y(t) gives
y(\omega) = \sum_k |c_k|^2\left[\frac{1}{\omega_k-\omega-i0}+\frac{1}{\omega_k+\omega+i0}\right]f(\omega).
This defines the response function \chi(\omega) \chi(\omega)\equiv \frac{y(\omega)}{f(\omega)} = \sum_k |c_k|^2\left[\frac{1}{\omega_k-\omega-i0}+\frac{1}{\omega_k+\omega+i0}\right]
Then use…
\text{Im} \frac{1}{x\mp i0} = \pm\pi\delta(x),
\operatorname{Im}\chi(\omega) =\mathrm{sgn}(\omega)\pi\sum_k |c_k|^2\delta(\omega_k-\omega)
- S(\omega) and \operatorname{Im}\chi(\omega) are then related by
S(\omega) = 2\operatorname{Im}\chi(\omega)\left[n_\text{B}(\omega)+1\right]
- This is a quantum fluctuation dissipation relation
Check
Check that in the classical limit (k_\text{B}T\gg \hbar \omega) S(\omega) = 2\operatorname{Im}\chi(\omega)\left[n_\text{B}(\omega)+1\right] reduces to S(\omega)=\frac{2k_\text{B}T}{\omega} \operatorname{Im}\chi(\omega) Consistent with classical equipartition
Golden Rule and Dissipation
We saw that classically \text{Im}\,\chi(\omega) related to dissipation
FDT relates \operatorname{Im}\chi(\omega) and S(\omega). How is S(\omega) related to dissipation?
Regard driving force as perturbation that causes transitions between energy eigenstates H_\text{pert} = - f(t)y with f(t)=f_0\cos\omega t
In lowest order perturbation theory, system makes transitions \pm\omega in energy
Rates found from Fermi’s golden rule
\Gamma_{n\to m} = 2\pi \left(\frac{f_0}{2}\right)^2|\langle{n}\rvert y\lvert{m}\rangle|^2 \delta(\pm\omega+E_m-E_n).
Total rate is sum over all initial (\lvert{n}\rangle) and final states (\lvert{m}\rangle), including probability e^{-\beta E_n}/Z of finding the system initially in \lvert{n}\rangle
c.f. spectral representation of S(\omega)
S(\omega) = 2\pi\sum_{m,n} \frac{e^{-\beta E_n}}{Z} |\langle{n}\rvert y\lvert{m}\rangle|^2 \delta(\omega-E_m+E_n)
\Gamma(\omega) = S(\omega)\left(\frac{f_0}{2}\right)^2
S(\omega) measures rate of transitions absorbing energy \omega; S(-\omega) the rate for emitting energy \omega.
Asymmetry of S(\omega) is asymmetry between emission and absorption of radiation
The rate of energy absorption is
\omega\Gamma(\omega) = \omega S(\omega)\left(\frac{f_0}{2}\right)^2 = \frac{1}{2}\omega\operatorname{Im}\chi(\omega)\left[n_\text{B}(\omega)+1\right]f_0^2
\omega\Gamma(\omega) = \omega S(\omega)\left(\frac{f_0}{2}\right)^2 = \frac{1}{2}\omega\operatorname{Im}\chi(\omega)\left[n_\text{B}(\omega)+1\right]f_0^2
Check
Compare with \begin{align*} W_\text{diss} = \langle f(t) \dot y(t)\rangle = \frac{1}{2}\omega\operatorname{Im}\chi(\omega)f_0^2 \end{align*} They agree when n_\text{B}(\omega)\to 0: energy of transition being much larger than thermal energy \hbar\omega\gg k_B T.
Linear Response: Formal Theory
So far, considered only response of linear systems!
How do we talk about linear response in general?
Kubo Formula
- How does observable A depend on \lambda_t, which appears (for small variations) linearly in the Hamiltonian
H_t = H_0 - \lambda_t B?
- B=-\frac{\partial H}{\partial \lambda} is generalized force; \lambda generalized displacement
In the interaction picture \lvert{\Psi_I(t)}\rangle \equiv e^{iH_0 t}\lvert{\Psi(t)}\rangle i\frac{\partial \lvert{\Psi_I(t)}\rangle}{\partial t} = -\lambda_t B_I(t) \lvert{\Psi_I(t)}\rangle, where B_I(t) = e^{iH_0 t}B e^{-iH_0 t}
Result of first order time dependent perturbation theory is \lvert{\Psi_I(t)}\rangle=\lvert{\Psi(0)}\rangle+\lvert{\Psi^{(1)}_I(t)}\rangle+\cdots, with
\lvert{\Psi^{(1)}_I(t)}\rangle = i\int_0^t dt' \lambda_{t'} B_I(t') \lvert{\Psi(0)}\rangle
\begin{align*} &\Braket{\Psi(t)|A|\Psi(t)} = \Braket{\Psi_I(t)|A_I(t) |\Psi_I(t)} \nonumber\\ &=\Braket{\Psi(0)|A_I(t)|\Psi(0)} +i \int_0^t dt' \lambda_{t'}\Braket{\Psi(0)| \left[A_I(t),B_I(t')\right] |\Psi(0)} \end{align*}
Mixed states can be treated by averaging over a distribution of quantum states \langle\cdots \rangle \longrightarrow \langle\langle\cdots\rangle\rangle
\chi_{AB}(t) of A due to perturbation that couples to B
\chi_{AB}(t) = i\langle\langle\left[A_I(t),B_I(0)\right]\rangle\rangle,\quad t>0. (Normally write A(t) rather than A_I(t): Heisenberg picture for the unperturbed problem)
- This is the Kubo formula. It expresses the response of a system in terms of the dynamics of the unperturbed system.
Fluctuation Dissipation Theorem (general)
- Start from the correlation function
S_{AB}(t) \equiv \langle\langle A_I(t)B_I(0)\rangle\rangle
- Recalling that \langle\langle\cdots \rangle\rangle = \frac{1}{Z}\mathop{\mathrm{tr}}\left[e^{-\beta H}\cdots\right], you should be able to show that
S_{AB}(t) = S_{BA}(-t-i\beta)
Check
Hint: use the cyclic property of the trace.
S_{AB}(t) = S_{BA}(-t-i\beta).
- Fourier transforming, we arrive at
S_{AB}(\omega) = e^{\beta\omega} S_{BA}(-\omega) (we’ve seen this before!)
- \chi_{AB}(t) (a commutator) can be written in terms of S_{AB}(\omega)
\begin{align*} \chi_{AB}(t) &= \begin{cases} i\left[S_{AB}(t)-S_{BA}(-t)\right] & t>0\\ 0 & t<0 \end{cases}\\ &= i\theta(t)\left[S_{AB}(t)-S_{BA}(-t)\right] \end{align*}
\chi_{AB}(t)=i\theta(t)\left[S_{AB}(t)-S_{BA}(-t)\right]
- \chi_{AB}(\omega) can then be expressed as the convolution. The Fourier transform of the step function is
\tilde\theta(\omega) = \frac{i}{\omega+i0} \begin{align*} \chi_{AB}(\omega)&= -\int \frac{d\omega'}{2\pi}\frac{S_{AB}(\omega')-S_{BA}(-\omega')}{\omega-\omega'+i0}\\ &=-\int \frac{d\omega'}{2\pi}\frac{S_{AB}(\omega')\left[1-e^{-\beta\omega'}\right]}{\omega-\omega'+i0} \end{align*}
- To make sense of this formula, use the Kramers–Kronig relation \begin{align*} \chi_{AB}(\omega) &=\operatorname{Re}\chi_{AB}(\omega) + i\operatorname{Im}\chi_{AB}(\omega)\\ &= \mathcal{P}\int_{-\infty}^\infty \frac{d\omega'}{\pi}\frac{\operatorname{Im}\chi_{AB}(\omega')}{\omega'-\omega} + i\operatorname{Im}\chi_{AB}(\omega)\\ &= \int_{-\infty}^\infty \frac{d\omega'}{\pi}\frac{\operatorname{Im}\chi_{AB}(\omega')}{\omega'-\omega-i0}, \end{align*} where we used \frac{1}{x+i0} = \mathcal{P}\frac{1}{x} -i\pi\delta(x)
- Finally! S_{AB}(\omega) = 2\operatorname{Im}\chi_{AB}(\omega)\left[n_\text{B}(\omega)+1\right]
Spectral Representation
The quantites \chi_{AB}(\omega) and S_{AB}(\omega) have spectral representations in terms of energy eigenstates and eigenvalues
S_{AB}(\omega) = 2\pi\sum_{m,n} \frac{e^{-\beta E_m}}{Z} \Braket{m|A|n}\Braket{n|B|m} \delta(\omega-E_n+E_m)
Check
Use the spectral representation to prove the fluctuation dissipation relation
- S_{AA}(\omega) can be interpreted in terms of Fermi golden rule, as we saw for oscillator. Notice that S_{AA}(\omega)>0
Response of Matter
- Back to many body physics!
Density Response
- Apply time dependent potential corresponding to term in Hamiltonian
H_\text{pert} = \sum_{j=1}^N V(\mathbf{r}_i,t) = \int V(\mathbf{r},t)\rho(\mathbf{r})\, d\mathbf{r}= \frac{1}{L^3}\sum_\mathbf{q}V_\mathbf{q}(t) \rho_{-\mathbf{q}}
Perturbation couples to the density: how is density affected?
In a translationally invariant system
\langle\langle \rho_\mathbf{q}(t)\rangle\rangle = -\frac{1}{L^3} \int_{-\infty}^t \chi^{\rho}_\mathbf{q}(t-t') V_\mathbf{q}(t)\,dt',
where the density response function \chi^\rho_\mathbf{q}(t) is
\chi_\rho(\mathbf{q},t) = i\langle\langle\left[\rho_\mathbf{q}(t),\rho_{-\mathbf{q}}(0)\right]\rangle\rangle
General theory applies with A=\rho_\mathbf{q} and B=\rho_{-\mathbf{q}}. At T=0 S_\rho(\mathbf{q},\omega) = 2\pi\sum_{n} |\langle{0}\rvert\rho_\mathbf{q}\lvert{n}\rangle|^2 \delta(\omega-E_n+E_0)
This is the dynamical structure factor, on account of its importance in scattering experiments.
The static structure factor is S_\rho(\mathbf{q}) = \int S_\rho(\mathbf{q},\omega) \frac{d\omega}{2\pi} = \langle\langle\rho_\mathbf{q}\rho_{-\mathbf{q}}\rangle\rangle
Sum rules
S_\rho(\mathbf{q},\omega) obeys certain general relations irrespective of system
If interaction depends only on density \left[H_\text{int},\rho_\mathbf{q}\right]=0
\left[H,\rho_\mathbf{q}\right]=\left[T,\rho_\mathbf{q}\right]
T = -\frac{1}{2m}\sum_{j=1}^N \nabla_i^2
- Taking \rho_\mathbf{q}=\sum_{j=1}^N e^{-i\mathbf{q}\cdot\mathbf{r}_j}, we find
[[H,\rho_\mathbf{q}],\rho_{-\mathbf{q}}] = -\frac{N\mathbf{q}^2}{m}
- Evaluate by introducing resolution of the identity \sum_n \lvert{n}\rangle\langle{n}\rvert=1
\begin{align*} \braket{0|[[H,\rho_\mathbf{q}],\rho_{-\mathbf{q}}]|0}&=\braket{0|H\rho_\mathbf{q}\rho_{-\mathbf{q}}- \rho_\mathbf{q}H\rho_{-\mathbf{q}}-\rho_{-\mathbf{q}} H\rho_\mathbf{q}+\rho_{-\mathbf{q}}\rho_\mathbf{q}H|0}\\ &=2\sum_n|\langle{0}\rvert\rho_\mathbf{q}\lvert{n}\rangle|^2\left(E_0-E_n\right) \end{align*}
- We can relate this to S(\mathbf{q},\omega) using spectral representation
S_\rho(\mathbf{q},\omega) = 2\pi\sum_{n} |\langle{0}\rvert\rho_\mathbf{q}\lvert{n}\rangle|^2 \delta(\omega-E_n+E_0) to give the f-sum rule
\int_{-\infty}^\infty \omega S(\mathbf{q},\omega) \frac{d\omega}{2\pi}= \frac{N\mathbf{q}^2}{2m}
Compressibility sum rule
- Compressibility
\beta=-\frac{1}{V}\frac{\partial V}{\partial p}. (inverse of Bulk modulus)
- p = -\frac{\partial E_0}{\partial V} at T=0. If E_0 = V \epsilon(\rho), then
\beta^{-1} = \rho^2 \epsilon''(\rho).
\beta^{-1} = \rho^2 \epsilon''(\rho).
- In the presence of a potential V(\mathbf{r}), energy density is
\epsilon(\rho_0+\delta\rho) = \frac{1}{2\beta\rho_0^2} \left[\delta\rho\right]^2 + V(\mathbf{r})\delta\rho
- Minimizing with respect to \delta\rho gives
\epsilon(V(\mathbf{r})) = - \frac{\beta\rho_0^2}{2} \left[V(\mathbf{r})\right]^2
- Compare with perturbation theory
- Change in energy due to perturbation
\sum_j V_0 \cos(\mathbf{q}\cdot \mathbf{r}_j) = \frac{V_0}{2}\left[\rho_\mathbf{q}+\rho_{-\mathbf{q}}\right]
- Second order perturbation theory for ground state E^{(2)} =\frac{V_0^2}{4} \sum_{n\neq 0} \frac{|\braket{0|\rho_\mathbf{q}|n}|^2}{E_0-E_n} =-\frac{V_0^2}{4}\int_0^\infty \frac{S(\mathbf{q},\omega)}{\omega}\frac{d\omega}{2\pi} (first order vanishes)
- Compare with
\epsilon(V(\mathbf{r})) = - \frac{\beta\rho_0^2}{2} \left[V(\mathbf{r})\right]^2
- This gives the compressibility sum rule at zero temperature
\lim_{\mathbf{q}\to 0}\int_0^\infty \frac{S(\mathbf{q},\omega)}{\omega}\frac{d\omega}{2\pi} = \frac{N\rho\beta}{2}.
- Compressibility sum rule often written in terms of speed of sound c = (\beta m \rho)^{-1/2}
\lim_{\mathbf{q}\to 0}\int_0^\infty \frac{S(\mathbf{q},\omega)}{\omega}\frac{d\omega}{2\pi} = \frac{N}{2mc^2}.
Single Mode Approximation
Some systems (e.g Bose gases), are well described by S_\rho(\mathbf{q},\omega) \sim 2\pi S_\rho(\mathbf{q}) \delta(\omega - \omega(\mathbf{q})), for low \mathbf{q}, where \omega(\mathbf{q}) is dispersion relation of collective excitations (e.g. Bogoliubov modes)
In this approximation, f-sum rule tells us that
S_\rho(\mathbf{q}) = \frac{N\mathbf{q}^2}{2m\omega(\mathbf{q})}.
Example 1: BEC (no interactions)
Excitations out of the condensate are free particles \omega(\mathbf{q}) = \frac{\mathbf{q}^2}{2m} S_\rho(\mathbf{q}) = N.
Completely uncorrelated particle positions (Poisson statistics).
Example 2: interacting BEC / elastic chain
- \omega(\mathbf{q}) = c|\mathbf{q}| i.e. linear dispersion with finite speed of sound
S_\rho(\mathbf{q}) = \frac{N|\mathbf{q}|}{2mc}.
- Density fluctuations vanish as wavevector goes to zero, indicating long-range correlations between positions in the ground state.
Check
Check compressibility sum rule
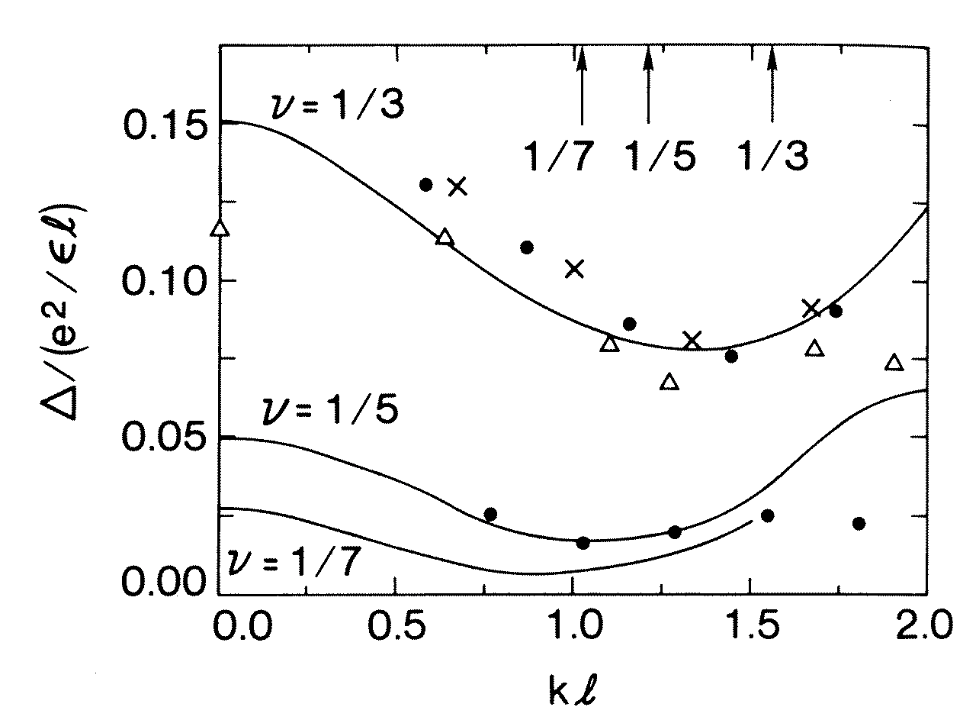
Example 3: FQHE
- Assuming single mode approximation
S_\rho(\mathbf{q},\omega) \sim 2\pi S_\rho(\mathbf{q}) \delta(\omega - \omega(\mathbf{q}))
- Can use S_\rho(\mathbf{q}) to find dispersion (see e.g. Girvin (2002) for FQHE)
\omega(\mathbf{q}) = \frac{N\mathbf{q}^2}{2m S_\rho(\mathbf{q})}
