Many Body Wavefunctions

Welcome!

About this course

• What can we solve in quantum mechanics?

  • Particle in a box
  • Harmonic oscillator H = -\frac{1}{2m}\left(\frac{d}{dx}\right)^2 +\frac{1}{2}m\omega^2 x^2
  • Hydrogen atom H = -\frac{1}{2m}\nabla^2 - \frac{e^2}{r}

• What would we like to solve?

Everything…

• Given ion positions \mathbf{R}_k, charge +Z_k e

H = -\frac{1}{2m}\sum_{j=1}^M\nabla^2_j + e^2\sum_{j<k}\frac{1}{|\mathbf{r}_j-\mathbf{r}_k|} - e^2\sum_{j<k}\frac{Z_k}{|\mathbf{r}_j-\mathbf{R}_k|}

• Want many-electron wavefunction \Psi(\mathbf{r}_1,\ldots \mathbf{r}_N)

• Hard for atoms / molecules: impossible for matter N\sim N_A!

• Goal: what is a solid / metal / superconductor / superfluid?

So what do we do?

• Use simple models that we can analyse in N\to\infty limit

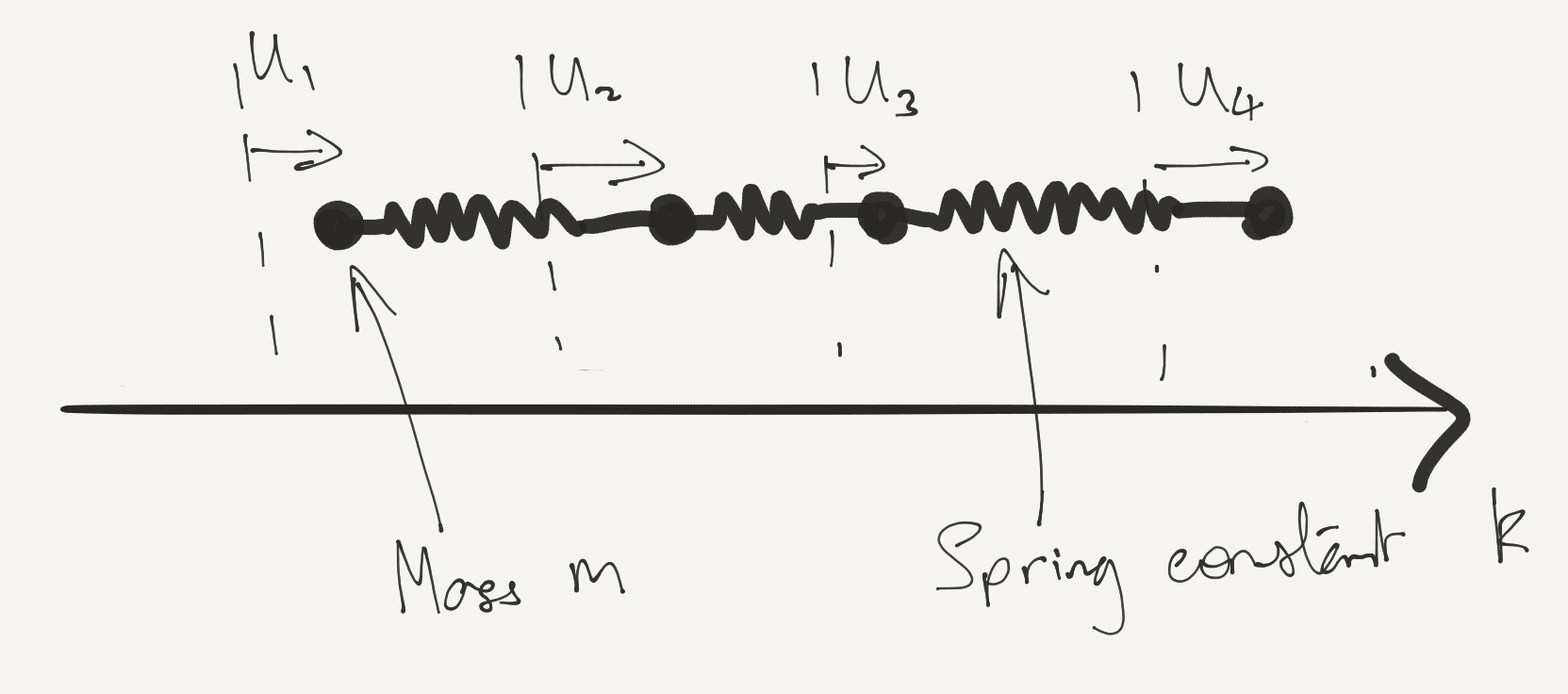
H = \sum_{j=1}^N \left[\frac{p_j^2}{2m} + \frac{k}{2} (u_j-u_{j+1})^2 \right]

• New techniques to represent wavefunctions and Hamiltonians (second quantization aka quantum field theory)

Housekeeping

• Course website tqm.tripos.org (updated with slides)

• Lecture capture

• Lectures are 90 minutes with 5 minute break roughly halfway

• Supervision in w/c 21/10, 4/11, 18/11, and 2/12. Details to follow

Check

Small exercises to check your understanding as you read the notes. Make sure you do them!

\hbar = 1!

Many Body Wavefunctions

This lecture is about the general character of many body wavefunctions and what they tell us, focusing on the simplest type: product states

Systems of indistinguishable particles are described by totally symmetric or totally antisymmetric wavefunctions

• The first kind are bosons, the second fermions

Two Particles

• In general described by \Psi(\mathbf{x},\mathbf{y})

• A pair of particles in states \lvert{\varphi_1}\rangle and \lvert{\varphi_2}\rangle

\Psi_\text{dist.}(\mathbf{r}_1,\mathbf{r}_2)\stackrel{?}{=} \varphi_1(\mathbf{r}_1)\varphi_2(\mathbf{r}_2)

• This would be fine for distinguishable particles

Accounting for symmetry

\Psi(\mathbf{r}_1,\mathbf{r}_2)=\frac{1}{\sqrt{2}}[\varphi_1(\mathbf{r}_1)\varphi_2(\mathbf{r}_2)\pm \varphi_2(\mathbf{r}_1)\varphi_1(\mathbf{r}_2)]

• upper sign for bosons and the lower for fermions

• 1/\sqrt{2} for normalization if \varphi_{1,2}(\mathbf{r}) are orthonormal

• When \varphi_1=\varphi_2 fermion \Psi(\mathbf{r}_1,\mathbf{r}_2) vanishes: exclusion principle

Independent Particles?

• Probability density is \rho_{12}(\mathbf{r}_1,\mathbf{r}_2)=|\Psi(\mathbf{r}_1,\mathbf{r}_2)|^2

• For distinguishable particles

\rho_{12}(\mathbf{r}_1,\mathbf{r}_2)=|\varphi_1(\mathbf{r}_1)\varphi_2(\mathbf{r}_2)|^2=\rho_1(\mathbf{r}_1)\rho_2(\mathbf{r}_2)

Check

Work it out for identical bosons and fermions. Show that \rho_{12}(\mathbf{r},\mathbf{r}) = 0 for fermions, and \rho_{12}(\mathbf{r},\mathbf{r}) = 2\rho_1(\mathbf{r})\rho_2(\mathbf{r}) for bosons.

• For identical particles

\begin{aligned} \rho_{12}(\mathbf{r}_1,\mathbf{r}_2) &= \frac{1}{2}\left[\rho_1(\mathbf{r}_1)\rho_2(\mathbf{r}_2)+\rho_1(\mathbf{r}_2)\rho_2(\mathbf{r}_1)\right] \\ &\pm\frac{1}{2}\left[\varphi^{}_1(\mathbf{r}_1)\varphi^*_2(\mathbf{r}_1)\varphi^{}_2(\mathbf{r}_2)\varphi^*_1(\mathbf{r}_2)+\varphi^{}_1(\mathbf{r}_2)\varphi^*_2(\mathbf{r}_2)\varphi^{}_2(\mathbf{r}_1)\varphi^*_1(\mathbf{r}_1)\right] \end{aligned}

• Identical particles in quantum mechanics are never truly independent

Hong–Ou–Mandel effect

• Two photons (bosons) approach a beam splitter from either side

• Start in orthogonal states, end up in orthogonal states e.g.

\begin{aligned} \lvert{\text{Left}}\rangle\to\frac{1}{\sqrt{2}}\left(\lvert{\text{Left}}\rangle+ \lvert{\text{Right}}\rangle\right)\\\\ \lvert{\text{Right}}\rangle\to\frac{1}{\sqrt{2}}\left(\lvert{\text{Left}}\rangle- \lvert{\text{Right}}\rangle\right) \end{aligned}

Check

If we start in \frac{1}{\sqrt{2}}[\varphi_\text{L}(\mathbf{r}_1)\varphi_\text{R}(\mathbf{r}_2)\pm \varphi_\text{R}(\mathbf{r}_1)\varphi_\text{L}(\mathbf{r}_2)] What state do we end up in?

For bosons (+ sign) the different terms may be represented

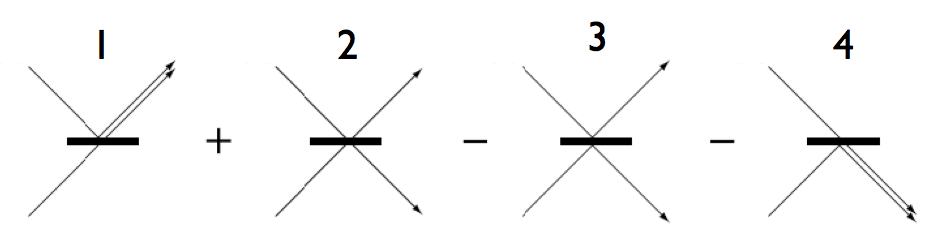
Noninteracting particles

H = \sum_{i=1}^{N} \overbrace{\left[-\frac{\nabla_i^{2}}{2m}+V(\mathbf{r}_i)\right]}^{\equiv H_\text{sp}\text{, single particle Hamiltonian}}

• H_\text{sp} has eigenstates \{\varphi_\alpha(\mathbf{r})\} and eigenenergies \{E_\alpha\}

• Eigenstate of N distinguishable particles \lvert{\Psi_{\alpha_{1}\alpha_{2}\cdots \alpha_{N}}}\rangle=\varphi_{\alpha_{1}}(\mathbf{r_{1}})\varphi_{\alpha_{2}}(\mathbf{r_{2}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{N}})

Check

Why is the energy

E = \sum_{j=1}^N E_{\alpha_j}?

Permutations

\Psi(\mathbf{r}_1,\mathbf{r}_2)=\frac{1}{\sqrt{2}}[\Psi_\text{dist.}(\mathbf{r}_1,\mathbf{r}_2) \pm \Psi_\text{dist.}(\mathbf{r}_2,\mathbf{r}_1)] % \varphi_1(\br_1)\varphi_2(\br_2)\pm \varphi_2(\br_1)\varphi_1(\br_2)]

• For more particles we have to include all possible permutations

• N! permutations of N objects

• A permutation \pi may be represented by a reordering of 1,\ldots N

• e.g. \pi=(312) for N=3

• Equivalently a function \pi of 1,\ldots N: \pi(1)=3, \pi(2)=1, \pi(3)=2

Signature of Permutation

• \mathrm{sgn}(\pi) is the signature of the permutation

• \pm1 for \pi involving an even (odd) number of exchanges

Symmetrize / Antisymmetrize

\mathcal{S}=\frac{1}{N!}\sum_{\pi} P_\pi, \qquad \mathcal{A}=\frac{1}{N!}\sum_{\pi} \mathrm{sgn}(\pi)P_\pi

• P_\pi is permutation operator for permutation \pi

• For two particles there are two permutations: \pi=(12) and \pi=(21)

P_{(21)}\Psi(\mathbf{r}_1,\mathbf{r}_2) = \Psi(\mathbf{r}_2,\mathbf{r}_1)

Symmetric and antisymmetric product states

\begin{aligned} \lvert{\Psi^{S}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle&=\sqrt{\frac{N!}{\prod_{\alpha}N_{\alpha}!}}\mathcal{S}\,\varphi_{\alpha_{1}}(\mathbf{r_{1}})\varphi_{\alpha_{2}}(\mathbf{r_{2}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{N}}) \nonumber \\ \lvert{\Psi^{A}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle&=\sqrt{N!}\mathcal{A}\,\varphi_{\alpha_{1}}(\mathbf{r_{1}})\varphi_{\alpha_{2}}(\mathbf{r_{2}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{N}}) \end{aligned}

• Occupation numbers \{N_{\alpha}\} give number of particles in state \alpha

• Explicitly:

\begin{aligned} \lvert{\Psi^{S}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle&=\sqrt{\frac{1}{N!\prod_{\alpha}N_{\alpha}!}}\sum_\pi\varphi_{\alpha_{1}}(\mathbf{r_{\pi(1)}})\varphi_{\alpha_{2}}(\mathbf{r_{\pi(2)}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{\pi(N)}})\\ \lvert{\Psi^{A}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle&=\sqrt{\frac{1}{N!}}\sum_\pi \mathrm{sgn}(\pi)\varphi_{\alpha_{1}}(\mathbf{r_{\pi(1)}})\varphi_{\alpha_{2}}(\mathbf{r_{\pi(2)}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{\pi(N)}}) \end{aligned}

• Note that it doesn’t matter if we permute coordinates or state labels \alpha_i

\lvert{\Psi^{S}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle=\sqrt{\frac{1}{N!\prod_{\alpha}N_{\alpha}!}}\sum_\pi\varphi_{\alpha_{\pi(1)}}(\mathbf{r_{1}})\varphi_{\alpha_{\pi(2)}}(\mathbf{r_2})\cdots\varphi_{\alpha_{\pi(N)}}(\mathbf{r_N})

Check

Show that these are normalized wavefunctions if the single particle state \lvert{\varphi_\alpha}\rangle are orthonormal

Occupation Numbers

• State is characterized only by occupation numbers \{N_{\alpha}\}. Use these as a label instead

• Caution: To fix the sign of the fermion wavefunction, have to choose an order e.g. \varphi_{\alpha_{1}}(\mathbf{r_{1}})\varphi_{\alpha_{2}}(\mathbf{r_{2}})\cdots\varphi_{\alpha_{N}}(\mathbf{r_{N}})

• The total energy is

E=\sum_{i=1}^{N}E_{\alpha_{i}}=\sum_{\alpha}N_{\alpha} E_{\alpha}

Slater Determinant

• The fermion product state is a determinant!

\lvert{\Psi^{A}_{\alpha_{1}\alpha_{2}\cdots\alpha_{N}}}\rangle=\frac{1}{\sqrt{N!}}\begin{vmatrix} \varphi_{\alpha_{1}}(\mathbf{r_{1}}) & \varphi_{\alpha_{1}}(\mathbf{r_{2}}) & \cdots & \varphi_{\alpha_{1}}(\mathbf{r_{N}}) \\ \varphi_{\alpha_{2}}(\mathbf{r_{1}}) & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \varphi_{\alpha_{N}}(\mathbf{r_{1}}) & \cdots & \cdots & \varphi_{\alpha_{N}}(\mathbf{r_{N}}) \end{vmatrix}

• Vanishes when two rows or two columns are identical
  • Zero if two particle coordinates coincide (\mathbf{r}_{i}=\mathbf{r}_{j})
  • Zero if two particles occupy the same state (\alpha_{i}=\alpha_{j})

Noninteracting particles on a ring

• Ring has circumference L. Single particle eigenstates

\varphi_{n}(x)=\frac{1}{\sqrt{L}}\exp\left(ik_n x\right)

• k_n=\frac{2\pi n}{L}, n\in\mathbb{Z}. Energies are E_{n}=\frac{k_n^2}{2m}

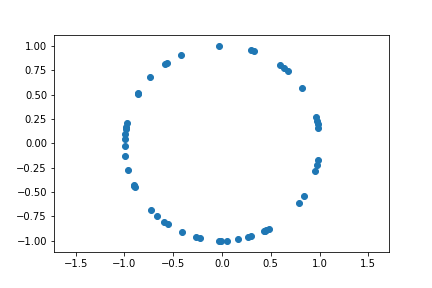
Ground State of Bosons

• Every particle in the state \lvert{\varphi_{0}}\rangle with zero energy: N_{0}=N

\Psi^{S}(x_{1},x_{2},\ldots x_{N})=\frac{1}{L^{N/2}}

• That was easy! The fermion case is harder

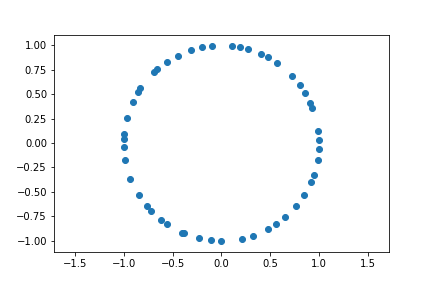
Ground State of Fermions

• Fill each level with one particle, starting at the bottom (Fermi sea)

  • N odd: n=-(N-1)/2, -(N-3)/2,\ldots, -1, 0, 1 \ldots (N-1)/2

  • N even: decide whether to put the last particle at n=\pm N/2

Complex notation

z_{i}=\exp(2 \pi i x_{i}/L)

• The Slater determinant is

\Psi_0(x_1,\ldots, x_N)=\begin{vmatrix} z_{1}^{-(N-1)/2} & z_{2}^{-(N-1)/2} & \cdots & z_{N}^{-(N-1)/2} \\ z_{1}^{-(N-3)/2} & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ z_{1}^{(N-1)/2} & \cdots & \cdots & z_{N}^{(N-1)/2} \end{vmatrix}

Simple example N=3

\begin{aligned} \Psi_0(x_1,x_2,x_3)&=\begin{vmatrix} z_{1}^{-1} & z_{2}^{-1} & z_{3}^{-1} \\ 1 & 1 & 1 \\ z_{1} & z_{2} & z_{3} \end{vmatrix} = \frac{z_{1}}{z_{2}}-\frac{z_{2}}{z_{1}}+\frac{z_{3}}{z_{1}}-\frac{z_{1}}{z_{3}}+\frac{z_{2}}{z_{3}}-\frac{z_{3}}{z_{2}}\nonumber\\ &=\left(\sqrt{\frac{z_{3}}{z_{1}}}-\sqrt{\frac{z_{1}}{z_{3}}}\right)\left(\sqrt{\frac{z_{1}}{z_{2}}}-\sqrt{\frac{z_{2}}{z_{1}}}\right)\left(\sqrt{\frac{z_{2}}{z_{3}}}-\sqrt{\frac{z_{3}}{z_{2}}}\right) \nonumber\\ &\propto \sin\left(\frac{ \pi[x_{1}-x_{2}]}{L}\right)\sin\left(\frac{ \pi[x_{3}-x_{1}]}{L}\right)\sin\left(\frac{ \pi[x_{2}-x_{3}]}{L}\right) \end{aligned}

• Wavefunction vanishes x_{i}=x_{j}

Check

Check it is periodic and totally antisymmetric

Generalization for N odd

\Psi_0(x_1,\ldots, x_N)\propto\prod_{i<j}^{N} \sin\left(\frac{\pi[x_{i}-x_{j}]}{L}\right)

Check

Show this using the Vandermonde determinant \begin{vmatrix} 1 & 1 & \cdots & 1 \\ z_{1} & z_{2} & \cdots & \cdots \\ z_{1}^{2} & z_{2}^{2} & \cdots & \cdots \\ z_{1}^{N-1} & z_{2}^{N-1} & \cdots & z_{N}^{N-1} \end{vmatrix}=\prod_{i<j}^{N}(z_{j}-z_{i})

Terminology

• The wavevector of the last fermion added is called the Fermi wavevector k_\text{F}

• Here k_\text{F}=\frac{(N-1)\pi}{L}

• Fermi energy E_{F}=\frac{k_\text{F}^{2}}{2m} is the corresponding energy

Probability distribution

• For boson ground state \Psi is constant, so is |\Psi|^2

• For fermions

Marginal distributions

• One particle distribution is related to average density of particles \rho_1(x_1) = N \int dx_2\ldots dx_N \lvert\Psi(x_1,x_2,\ldots,x_N)\rvert^2

• Note that density is always a number density (not mass density)

• Normalization of the wavefunction implies \int dx \rho_1(x) = N

• In a translationally invariant system like the fermion gas on a ring we expect the average density to be constant

Density Operator

• Regard \rho_1(x_1) as an expectation of a density operator \rho(x) = \sum_j \delta(x-x_j) so that \rho_1(x) = \langle{\Psi}\rvert \rho(x) \lvert \Psi \rangle

Single particle density matrix

g(x,y) \equiv N\int dx_2\ldots dx_N \Psi^{}(x,x_2,\ldots,x_N)\Psi^{*}(y,x_2,\ldots,x_N)

• Note g(x,x) = \rho_1(x)

Check

Starting from the Slater determinant, show that g(x,y) for the ground state of the Fermi gas is \begin{aligned} g(x,y) &= \frac{1}{L}\sum_{|k|<k_\text{F}} e^{ik(x-y)} \longrightarrow \int_{-k_\text{F}}^{k_\text{F}} \frac{dk}{2\pi} e^{ik(x-y)} \\ &\longrightarrow n \frac{\sin \left[k_\text{F}(x-y)\right]}{k_\text{F}(x-y)} \end{aligned} where n \equiv \frac{k_\text{F}}{\pi} is the average density

Pair Distribution

• Marginal probability distribution of a pair of particles \rho_2(x_1,x_2) = N(N-1) \int dx_3\ldots dx_N\left|\Psi(x_1,x_2,\ldots,x_N)\right|^2
• The prefactor is to account for all pairs of particles

Check

Starting from the Slater determinant, show that \rho_2(x_1,x_2) = n^2\left[1 - \left(\frac{\sin\left[k_\text{F}(x_1-x_2)\right]}{k_\text{F}(x_1-x_2)}\right)^2\right] This vanishes at x_1=x_2

Impenetrable Bose Gas

H = -\frac{1}{2m}\sum_j \frac{\partial^2}{\partial x_j^2} + \overbrace{c\sum_{j<k}\delta(x_j-x_k)}^{\equiv H_\text{int}}

• The second term is interaction between pairs of particles

• For fermions, the interaction has no effect at all (\delta-function)!

• For bosons with c\to \infty: eigenenergies coincide with those of free fermions, and eigenstates are modulus of fermion eigenstates

Check

Why?

Ground state

\Psi_0(x_1,\ldots, x_N) = \prod_{i<j}^{N} \left|\sin\left(\frac{\pi[x_{i}-x_{j}]}{L}\right)\right|

• Can calculate any observable as long as it’s insensitive to taking the modulus (e.g. average density and pair distribution)