Bose Gas
Bose Gas
- Noninteracting bosons form a Bose–Einstein condensate (BEC)
- What do interactions do?
- BEC closely related to superfluidity
Gross–Pitaevskii Approximation
Variational appraoch to Bose gas (c.f. Hartree–Fock)
Put all particles in same single particle state!
\Psi(\mathbf{r}_1,\ldots \mathbf{r}_N) = \prod_{j=1}^N \varphi_0(\mathbf{r}_i)= \frac{1}{\sqrt{N!}}\left(a^\dagger(\varphi_0)\right)^N\lvert{\text{VAC}}\rangle
- State with macroscopic number of particles in a single particle state is a Bose condensate
- For the non-interacting Hamiltonian
H = \sum\left[-\frac{\nabla_i^2}{2m} + V(\mathbf{r}_i)\right]
- Ground state is exactly \Psi(\mathbf{r}_1,\ldots \mathbf{r}_N) = \prod_{j=1}^N \varphi_0(\mathbf{r}_i)= \frac{1}{\sqrt{N!}}\left(a^\dagger(\varphi_0)\right)^N\lvert{\text{VAC}}\rangle, with \varphi_0(\mathbf{r}) the ground state of single particle Hamiltonian
- Add interaction
\begin{align*} H_\text{int.} &= \sum_{j<k} U(\mathbf{r}_j-\mathbf{r}_k) \\ &= \frac{1}{2}\int d\mathbf{r}_1 d\mathbf{r}_2\, U(\mathbf{r}_1-\mathbf{r}_2)\psi^\dagger(\mathbf{r}_1)\psi^\dagger(\mathbf{r}_2)\psi^{\vphantom{\dagger}}(\mathbf{r}_2)\psi^{\vphantom{\dagger}}(\mathbf{r}_1) \end{align*}
Ground state is more complicated, but can use BEC form with \varphi_0(\mathbf{r}) as a variational function
Optimal \varphi_0(\mathbf{r}) obeys Gross–Pitaevskii equation
Gross–Pitaevskii Equation
Take short-ranged interactions for simplicity U(\mathbf{r}-\mathbf{r}') = U_0\delta(\mathbf{r}-\mathbf{r}')
For variational calculation we need
\langle E \rangle = \frac{\braket{\Psi|H|\Psi}}{\braket{\Psi|\Psi}}
- Minimize \braket{\Psi|H|\Psi} and fix norm. using Lagrange multiplier
\begin{align*} \Braket{\Psi|H|\Psi}=N \int d\mathbf{r}\left[\frac{1}{2m}|\nabla\varphi_0|^2+V(\mathbf{r})|\varphi_0(\mathbf{r})|^2 \right]\\ +\frac{1}{2}N(N-1)U_0\int d\mathbf{r}|\varphi_0(\mathbf{r})|^4 \end{align*}
Neglect difference between N and N+1 \begin{align*} \Braket{\Psi|H|\Psi}=N \int d\mathbf{r}\left[\frac{1}{2m}|\nabla\varphi_0|^2+V(\mathbf{r})|\varphi_0(\mathbf{r})|^2 \right]\\ +\frac{1}{2}N^2 U_0\int d\mathbf{r}|\varphi_0(\mathbf{r})|^4 \end{align*}
Extremize the functional
\Braket{\Psi|H|\Psi} - \mu N \int d\mathbf{r}|\varphi_{0}(\mathbf{r})|^{2}
- Calculus of variations yields
\left[-\frac{1}{2m}\nabla^2-\mu+V(\mathbf{r})+NU_0|\varphi_0(\mathbf{r})|^2\right]\varphi_0(\mathbf{r})=0
Define \varphi(\mathbf{r})\equiv\sqrt{N}\varphi_{0}(\mathbf{r})
\varphi(\mathbf{r}) is condensate wavefunction or order parameter. Obeys Gross–Pitaevskii equation
\left[-\frac{1}{2m}\nabla^2-\mu+V(\mathbf{r})+U_0|\varphi(\mathbf{r})|^2\right]\varphi(\mathbf{r})=0
Fix Lagrange multiplier \mu by \int d\mathbf{r}\lvert{\varphi(\mathbf{r})}\rvert^{2}=N
\Braket{\Psi|H|\Psi}- \mu \int d\mathbf{r}\lvert{\varphi(\mathbf{r})}\rvert^{2}=\Braket{\Psi|H-\mu \mathsf{N}|\Psi} was extremized under general variations, including change in N \mu=\frac{\partial\braket{\Psi|H|\Psi}}{\partial N} Thus, \mu is identified with the chemical potential
Healing length
- 1D, no potential
\left[-\frac{1}{2m}\partial_x^2-\mu+U_0|\varphi|^2\right]\varphi(x)=0
- Dimensionless form \varphi(\mathbf{r})=\sqrt{n}\phi(\mathbf{r}/\xi) for \mu=U_0n
-\frac{1}{2m \xi^2}\phi''+\mu (|\phi|^2-1)\phi(x)=0
- If we set \xi\equiv \frac{1}{\sqrt{2m \mu}}=\frac{1}{\sqrt{2m n U_0}} then
-\phi''+(|\phi|^2-1)\phi(x)=0
- Healing length \xi is scale on which \varphi(\mathbf{r}) disturbed by localized perturbation of scale \ll \xi
Check
Near a wall \varphi(x)=\varphi_{\infty}\tanh \frac{x}{\sqrt{2}\xi}
where x is distance from wall, and \varphi_{\infty}=\sqrt{n} is fixed by the density far away.
Condensate in a Can

Some Observables
- Density and current density
\begin{align*} \rho(\mathbf{r})&=|\varphi(\mathbf{r})|^2,\\ \mathbf{j}(\mathbf{r})&=-\frac{i}{2m}\left[\varphi^{*}(\mathbf{r})\left(\nabla\varphi(\mathbf{r})\right)-\left(\nabla\varphi^{*}(\mathbf{r})\right)\varphi(\mathbf{r})\right] \end{align*}
- Useful decomposition into magnitude and phase
\varphi(\mathbf{r})=\sqrt{\rho(\mathbf{r})}e^{i\chi(\mathbf{r})}
- Using \mathbf{j}=\rho \mathbf{v} we get superfluid velocity
\mathbf{v}_{s}\equiv\frac{1}{m}\nabla\chi
Example: Vortex
Expect \mathbf{v}_{s}=\frac{1}{m}\nabla\chi to be irrotational \nabla\times \mathbf{v}_s = 0,
Equivalently to have vanishing circulation around any closed loop
\oint \mathbf{v}_s\cdot d\mathbf{l}=0
- Phase can increase by a multiple of 2\pi around a closed loop, so \oint \mathbf{v}_s\cdot d\mathbf{l}=\frac{2\pi \ell}{m},\quad \ell\in\mathbb{Z} This is the Onsager–Feynmann quantization condition
Localized configuration with finite circulation is a vortex in fluid dynamics
In normal fluid there is no reason for the vorticity to be quantized \oint \mathbf{v}_s\cdot d\mathbf{l}=\frac{h\ell}{m},\quad \ell\in\mathbb{Z}, shows that this is a truly quantum phenomenon.
A non-zero winding of phase requires that \rho(\mathbf{r}) vanishes at a point (in 2D) or on a line (in 3D)
- Look for 2D solutions where phase winds \ell times around origin
\varphi(r,\theta)\xrightarrow{r\to\infty} \sqrt{n} e^{i\ell\theta}
- Parameterize \varphi(r,\theta) = \sqrt{n} f(r/\xi)e^{i\ell\theta} to give an equation in s\equiv r/\xi (set \mu=U_0 n as before).
-f'' -\frac{f'}{s} + \frac{\ell^2 f}{s^2} - f +f^3 =0.
Check
Without finding the solution explicitly, show that f(s)\sim s^\ell for small s, and f(s\to\infty) \to 1.
Region of suppressed density size \xi, is vortex core
In three dimensions, vortex core is a line
Find energy of vortex by substituting solution back into energy
\begin{align*} \Braket{\Psi|H|\Psi}=\int d\mathbf{r}\left[\frac{1}{2m}|\nabla\varphi|^2+V(\mathbf{r})|\varphi(\mathbf{r})|^2 \right]+\frac{1}{2}U_0\int d\mathbf{r}|\varphi(\mathbf{r})|^4 \end{align*}
- Excess energy (relative to uniform state of density n)
\Delta E = \int d\mathbf{r}\left[\frac{n^2}{2m\xi^2}(f')^2+\frac{U}{2}n^2 \left(f^2-1\right)^2\right] + \frac{n^2}{2m}\int d\mathbf{r}\, f^2(\nabla\chi)^2
\Delta E = \int d\mathbf{r}\left[\frac{n^2}{2m\xi^2}(f')^2+\frac{U}{2}n^2 \left(f^2-1\right)^2\right] + \frac{n^2}{2m}\int d\mathbf{r}\, f^2(\nabla\chi)^2
First integral is finite: due to density \neq bulk value
Second is KE contribution from winding of vortex
\nabla \chi = \frac{\ell}{r}\hat{\mathbf{e}}_\theta,
- This contribution to the energy is logarithmically divergent
\Delta E = \text{const.} + \frac{\pi n \ell^2}{m}\log\left(\frac{L}{\xi}\right)
- Far-reaching analogy between superfluid velocity fields of vortices and magnetostatics of current-carrying wires,
| Vortices | Magnetostatics |
|---|---|
| Vortex cores | Wires |
| Superfluid velocity \mathbf{v}_s | Magnetic field, \mathbf{B} |
| Kinetic Energy | Magnetostatic Energy |
- Vortices with \lvert{\ell}\rvert>1 generally unstable: break into multiple vortices of winding \ell=\pm 1
- Like vortices repel each other, and can form spectacular vortex lattices, akin to crystals.
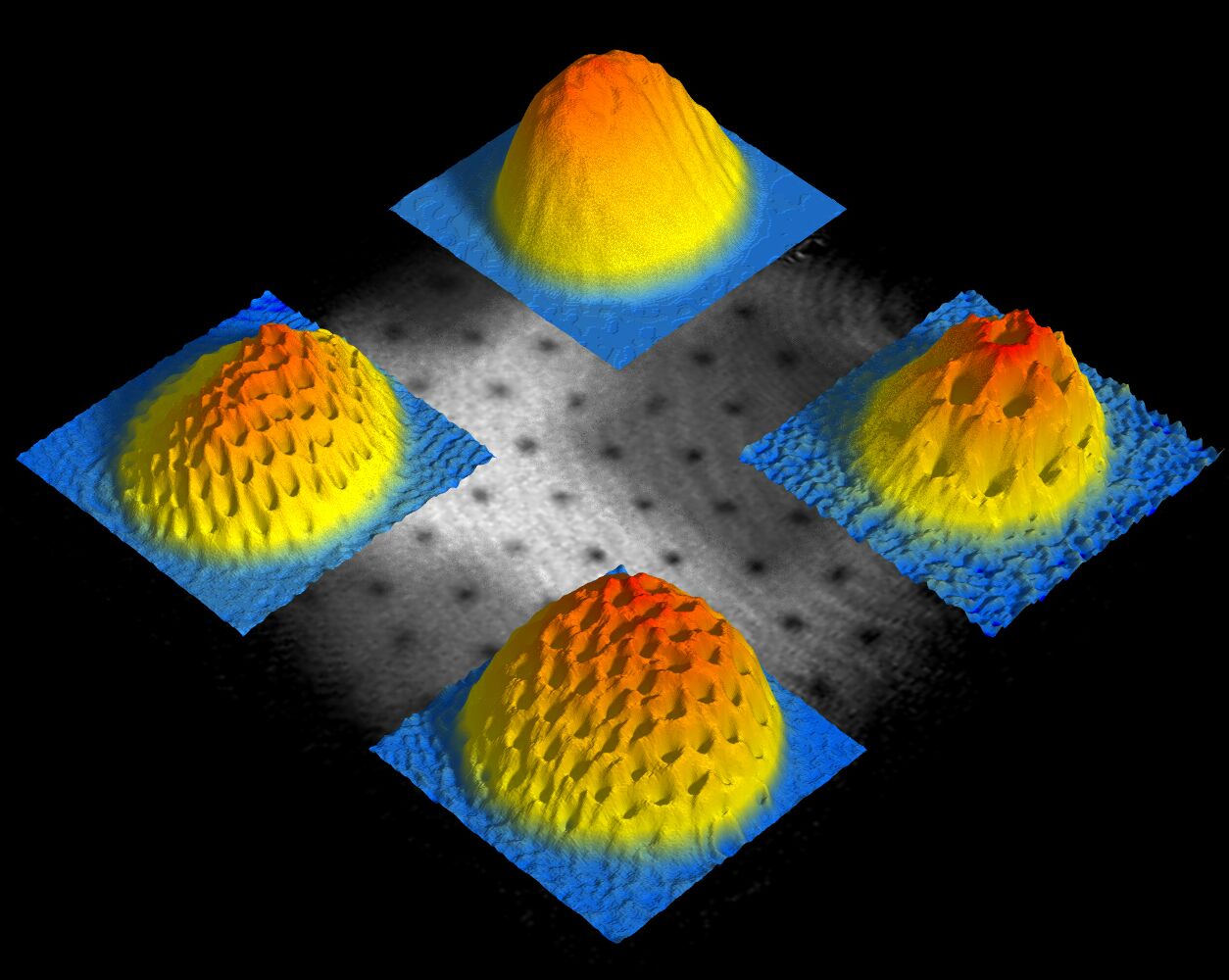
- Vortices are one manifestation of superfluidity
Bogoliubov Theory
How can we improve Gross–Pitaevskii approximation?
What about excited states?
From now on… uniform condensate with no V(\mathbf{r})=0
H =\sum_\mathbf{k}\epsilon(\mathbf{k})a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+ \overbrace{\frac{U_0}{2V}\sum_{\mathbf{k}_1+\mathbf{k}_2=\mathbf{k}_3+\mathbf{k}_4} a^\dagger_{\mathbf{k}_1}a^\dagger_{\mathbf{k}_2}a^{\vphantom{\dagger}}_{\mathbf{k}_3}a^{\vphantom{\dagger}}_{\mathbf{k}_4}}^{\equiv H_\text{int}}, - \epsilon(\mathbf{k})=\mathbf{k}^2/2m, and V the volume
GP approximation to ground state is \lvert{\Psi_\text{GP}}\rangle = \frac{1}{\sqrt{N!}}\left(a^\dagger_0\right)^N\lvert{\text{VAC}}\rangle
Act with H_\text{int}: only terms that contribute have \mathbf{k}_3=\mathbf{k}_4=0
H_\text{int}\lvert{\Psi_\text{GP}}\rangle = \frac{U_0}{2V}\sum_{\mathbf{k}} a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0}\lvert{\Psi_\text{GP}}\rangle
- For a better wavefunction, need to add some (\mathbf{k}, -\mathbf{k}) pairs!
Bogoliubov Hamiltonian
When interactions weak, expect true ground state close to \lvert{\Psi_\text{GP}}\rangle
Most particles in zero momentum state, with few (\mathbf{k}, -\mathbf{k}) pairs
Remember that
a^{\vphantom{\dagger}}\lvert{N}\rangle = \sqrt{N}\lvert{N-1}\rangle,\quad a^\dagger\lvert{N}\rangle = \sqrt{N+1}\lvert{N+1}\rangle,
- A term in H_\text{int} with a^{\vphantom{\dagger}}_0 or a^\dagger_0 is more important than one without. Arrange Hamiltonian by occurrences of a^{\vphantom{\dagger}}_0, a^\dagger_0
\begin{align*} H_\text{int} = \frac{U_0}{2V}a^\dagger_0a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_0 + \frac{U_0}{2V}\sum_{\mathbf{k}\neq0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0} + a^\dagger_{0}a^\dagger_{0}a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+4a^\dagger_\mathbf{k}a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_\mathbf{k}\right]\\\nonumber +\frac{U_0}{V}\sum_{\substack{\mathbf{k}_1=\mathbf{k}_2+\mathbf{k}_3\\ \mathbf{k}_{1,2,3}\neq 0}}\left[a^\dagger_{\mathbf{k}_3}a^\dagger_{\mathbf{k}_2}a^{\vphantom{\dagger}}_{\mathbf{k}_1}a^{\vphantom{\dagger}}_0 +a^\dagger_0a^\dagger_{\mathbf{k}_1}a^{\vphantom{\dagger}}_{\mathbf{k}_2}a^{\vphantom{\dagger}}_{\mathbf{k}_3}\right]+\frac{U_0}{2V}\sum_{\substack{\mathbf{k}_1+\mathbf{k}_2=\mathbf{k}_3+\mathbf{k}_4\\ \mathbf{k}_{1,2,3,4}\neq 0}} a^\dagger_{\mathbf{k}_1}a^\dagger_{\mathbf{k}_2}a^{\vphantom{\dagger}}_{\mathbf{k}_3}a^{\vphantom{\dagger}}_{\mathbf{k}_4} \end{align*}
Gross–Pitaevskii approximation corresponds to the first term
We now keep second term, and neglect third and fourth
\begin{align*} H_\text{pair} &= \sum_\mathbf{k}\epsilon(\mathbf{k})a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+\frac{U_0}{2V}a^\dagger_0a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_0 \nonumber\\ &\quad+\frac{U_0}{2V}\sum_{\mathbf{k}\neq0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0} + a^\dagger_{0}a^\dagger_{0}a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+4a^\dagger_\mathbf{k}a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*}
\begin{align*} H_\text{pair} &= \sum_\mathbf{k}\epsilon(\mathbf{k})a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+\frac{U_0}{2V}a^\dagger_0a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_0 \nonumber\\ &\quad+\frac{U_0}{2V}\sum_{\mathbf{k}\neq0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0} + a^\dagger_{0}a^\dagger_{0}a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+4a^\dagger_\mathbf{k}a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*}
- Rewrite second term using a^\dagger_0a^{\vphantom{\dagger}}_0 = N - N', with N'\equiv \sum_{\mathbf{k}\neq 0} N_\mathbf{k}
- Then a^\dagger_0a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_0 = N(N-1) - 2N'N_0+O(N_0^0 )
\begin{align*} H_\text{pair} = &N\epsilon(0)+\frac{U_0}{2V}N(N-1) +\sum_{\mathbf{k}\neq 0}\left[\epsilon(\mathbf{k})-\epsilon(0)\right]a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}\\ &+\frac{U_0}{2V}\sum_{\mathbf{k}\neq 0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0} + a^\dagger_{0}a^\dagger_{0}a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+2a^\dagger_\mathbf{k}a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*}
\begin{align*} H_\text{pair} = &N\epsilon(0)+\frac{U_0}{2V}N(N-1) +\sum_{\mathbf{k}\neq 0}\overbrace{\left[\epsilon(\mathbf{k})-\epsilon(0)\right]}^{\equiv\tilde\epsilon(\mathbf{k})}a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}\\ &+\frac{U_0}{2V}\sum_{\mathbf{k}\neq 0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}a^{\vphantom{\dagger}}_{0}a^{\vphantom{\dagger}}_{0} + a^\dagger_{0}a^\dagger_{0}a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+2a^\dagger_\mathbf{k}a^\dagger_0a^{\vphantom{\dagger}}_0a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*}
Weird trick alert! Replace a^\dagger_0, a^{\vphantom{\dagger}}_0 with \sqrt{N}, giving quadratic Hamiltonian (that we can solve)
- Resulting Hamiltonian no longer conserves particle number
Let’s see why this is a good approximation.
Consider action of Hamiltonian on state of form \lvert{\Psi'}\rangle\otimes\lvert{N_0}\rangle_0
a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_0\lvert{\Psi'}\rangle\otimes\lvert{N_0}\rangle_0 = \left(a^\dagger_\mathbf{k}\lvert{\Psi'}\rangle\right)\otimes a^{\vphantom{\dagger}}_0\lvert{N_0}\rangle_0 = \left(a^\dagger_\mathbf{k}\lvert{\Psi'}\rangle\right)\otimes \sqrt{N_0}\lvert{N_0-1}\rangle_0 a^{\vphantom{\dagger}}_\mathbf{k}a^\dagger_0\lvert{\Psi'}\rangle\otimes\lvert{N_0}\rangle_0 = \left(a^{\vphantom{\dagger}}_\mathbf{k}\lvert{\Psi'}\rangle\right)\otimes a^\dagger_0\lvert{N_0}\rangle_0 = \left(a^{\vphantom{\dagger}}_\mathbf{k}\lvert{\Psi'}\rangle\right)\otimes \sqrt{N_0+1}\lvert{N_0+1}\rangle_0
Ignore the difference between N_0 and N_0+1
If N_0 doesn’t fluctuate much matrix elements of H_\text{pair} are approximately unchanged when replace operator with numbers
Result is Bogoliubov Hamiltonian \begin{align*} H_\text{pair} &= \sum_\mathbf{k}\tilde\epsilon(\mathbf{k})a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+\frac{U_0}{2V}N(N-1) \nonumber\\ &\quad+\frac{U_0n_0}{2}\sum_{\mathbf{k}\neq0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}} + a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+2a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*} n_0 = N_0/V is density of particles in zero momentum state
Hamiltonian diagonalized by Bogoliubov transformation
Bogoliubov transformation
- Suppose we have an operator
h = \epsilon\left[a^\dagger_1a^{\vphantom{\dagger}}_1+a^\dagger_2a^{\vphantom{\dagger}}_2\right] + \delta\left[a^\dagger_1a^\dagger_2+a^{\vphantom{\dagger}}_1a^{\vphantom{\dagger}}_2\right]
- Want to express h in terms of some new bosons b^{\vphantom{\dagger}}_{1,2} as h = \Omega\left[b^\dagger_1b^{\vphantom{\dagger}}_1+b^\dagger_2b^{\vphantom{\dagger}}_2\right] +\text{const.} (because then the spectrum is obvious)
h = \begin{pmatrix} a^\dagger_1 & a^{\vphantom{\dagger}}_2 \end{pmatrix} \begin{pmatrix} \epsilon & \delta \\\\ \delta & \epsilon \end{pmatrix} \begin{pmatrix} a^{\vphantom{\dagger}}_1 \\\\ a^\dagger_2 \end{pmatrix}-\epsilon
- Try to express new bosons linearly in terms of old \begin{pmatrix} b^{\vphantom{\dagger}}_1 \\\\ b^\dagger_2 \end{pmatrix}= \Lambda \begin{pmatrix} a^{\vphantom{\dagger}}_1 \\\\ a^\dagger_2 \end{pmatrix} \Lambda is some 2\times 2 matrix. What conditions should it satisfy?
\begin{pmatrix} b^{\vphantom{\dagger}}_1 \\\\ b^\dagger_2 \end{pmatrix}= \Lambda \begin{pmatrix} a^{\vphantom{\dagger}}_1 \\\\ a^\dagger_2 \end{pmatrix}
Check
If b^{\vphantom{\dagger}}_{1,2} satisfy usual commutation relations then \Lambda^\dagger \sigma_3 \Lambda = \sigma_3
\Lambda^\dagger \sigma_3 \Lambda = \sigma_3
- Following parameterization is sufficient for our h
\Lambda= \begin{pmatrix} \cosh\kappa & \sinh\kappa \\\\ \sinh\kappa & \cosh\kappa \end{pmatrix}
Notice differences from rotation matrix:
- Hyperbolic instead of trignometric functions
- No sign difference between the off digaonal elements.
h = \begin{pmatrix} a^\dagger_1 & a^{\vphantom{\dagger}}_2 \end{pmatrix} \begin{pmatrix} \epsilon & \delta \\\\ \delta & \epsilon \end{pmatrix} \begin{pmatrix} a^{\vphantom{\dagger}}_1 \\\\ a^\dagger_2 \end{pmatrix}-\epsilon
\begin{pmatrix} b^{\vphantom{\dagger}}_1 \\\\ b^\dagger_2 \end{pmatrix}= \begin{pmatrix} \cosh\kappa & \sinh\kappa \\\\ \sinh\kappa & \cosh\kappa \end{pmatrix} \begin{pmatrix} a^{\vphantom{\dagger}}_1 \\\\ a^\dagger_2 \end{pmatrix}
Check
\begin{align*} \tanh 2\kappa = \frac{\delta}{\epsilon},\qquad \Omega = \sqrt{\epsilon^2-\delta^2\nonumber}\\ h = \Omega\left[b^\dagger_1b^{\vphantom{\dagger}}_1+b^\dagger_2b^{\vphantom{\dagger}}_2\right] + \Omega - \epsilon. \end{align*} What happens if \delta>\epsilon? What changes if \begin{pmatrix} \epsilon & \delta \\\\ \delta & \epsilon \end{pmatrix}\longrightarrow \begin{pmatrix} \epsilon_1 & \delta \\\\ \delta & \epsilon_2 \end{pmatrix}?
- Apply to Bogoliubov Hamiltonian \begin{align*} H_\text{pair} &= \sum_\mathbf{k}\tilde\epsilon(\mathbf{k})a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+\frac{U_0}{2V}N(N-1) \nonumber\\ &\quad+\frac{U_0n_0}{2}\sum_{\mathbf{k}\neq0}\left[a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}} + a^{\vphantom{\dagger}}_{\mathbf{k}}a^{\vphantom{\dagger}}_{-\mathbf{k}}+2a^\dagger_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}\right] \end{align*}
\begin{align*} b^{\vphantom{\dagger}}_\mathbf{p}=a^{\vphantom{\dagger}}_\mathbf{p}\cosh\kappa_\mathbf{p}+a^\dagger_{-\mathbf{p}}\sinh\kappa_\mathbf{p}\nonumber\\ \tanh2\kappa_\mathbf{p}=\frac{n_0 U_0}{\tilde\epsilon(\mathbf{k})+n_0 U_0} \end{align*}
H=E_0+\sum_{\mathbf{p}\neq 0}\omega(\mathbf{p})b^\dagger_\mathbf{p} b^{\vphantom{\dagger}}_\mathbf{p}.
- \omega(\mathbf{p}) is the Bogoliubov dispersion relation
\omega(\mathbf{p}) = \sqrt{\tilde\epsilon(\mathbf{k})\left(\tilde\epsilon(\mathbf{k})+2U_0n_0\right)}
- Ground state energy is
E_0=\frac{1}{2}nU_0 N+\sum_{\mathbf{p}\neq 0}\frac{1}{2}\left[\omega(\mathbf{p})-\tilde\epsilon(\mathbf{k})-n_0U_0\right]
E_0=\frac{1}{2}nU_0 N+\sum_{\mathbf{p}\neq 0}\frac{1}{2}\left[\omega(\mathbf{p})-\tilde\epsilon(\mathbf{k})-n_0U_0\right]
- Annoyingly, this integral is divergent at high momenta because
\omega(\mathbf{p})\underset{|\mathbf{p}| \to \infty}{\longrightarrow} \tilde\epsilon(\mathbf{k}) + n_0 U_0 -\frac{(n_0 U_0)^2}{2\tilde\epsilon(\mathbf{k})}
We can cure the problem by writing \begin{align*} E_0&=\overbrace{\frac{1}{2}nU_0 N\left[1-\frac{1}{V}\sum_\mathbf{p}\frac{U_0}{2\tilde\epsilon(\mathbf{k})}\right]}^{\text{1st and 2nd order PT}}\\ &+\overbrace{\sum_{\mathbf{p}\neq 0}\frac{1} {2}\left[\omega(\mathbf{p})-\tilde\epsilon(\mathbf{k})-n_0U_0+ \frac{(n_0U_0)^2}{2\tilde\epsilon(\mathbf{k})}\right]}^{\text{finite}} \end{align*}
Term added and subtracted is contribution to the ground state energy in second order perturbation theory
See Appendix and Problem Set 2 for further discussion
The Ground State
- So far, ground state defined by condition that it is a vacuum of Bogoliubov excitations
b^{\vphantom{\dagger}}_\mathbf{k}\lvert{0}\rangle=\left(\cosh\kappa_\mathbf{k}a^{\vphantom{\dagger}}_\mathbf{k}+\sinh\kappa_\mathbf{k}a^\dagger_{-\mathbf{k}}\right)\lvert{0}\rangle=0.
- A state (unnormalized) that satisfies this condition is
\lvert{0}\rangle=\prod_{\mathbf{k}\neq 0} \exp\left(-\frac{1}{2}\left[\tanh\kappa_\mathbf{k}\right]a^\dagger_{\mathbf{k}}a^\dagger_{-\mathbf{k}}\right)\lvert{\Psi_\text{GP}}\rangle
Check
Show this. If you’ve seen coherent states before, remember that the state e^{\alpha a^\dagger}\lvert{\text{VAC}}\rangle is an eigenstate of a^{\vphantom{\dagger}} with eigenvalue \alpha.
- Recall that Fourier components of density operator are
\rho_\mathbf{q}= \sum_\mathbf{k}a^\dagger_{\mathbf{k}-\mathbf{q}}a^{\vphantom{\dagger}}_\mathbf{k}
- Most important terms: a^\dagger_{\mathbf{k}-\mathbf{q}} or a^{\vphantom{\dagger}}_\mathbf{k} acts on the condensate
\rho_\mathbf{q}\sim \sqrt{N}\left(a^\dagger_{-\mathbf{q}} + a^{\vphantom{\dagger}}_{\mathbf{q}}\right) = \sqrt{N}e^{-\kappa_\mathbf{q}} \left(b^\dagger_{-\mathbf{q}} + b^{\vphantom{\dagger}}_{\mathbf{q}}\right)
e^{-\kappa_\mathbf{q}} = \sqrt{\frac{\epsilon(\mathbf{q})}{\omega(\mathbf{q})}}
Density fluctuations in ground state \Braket{0|\rho_{-\mathbf{q}}\rho_{\mathbf{q}}|0} = N\frac{\epsilon(\mathbf{q})}{\omega(\mathbf{q})}\xrightarrow{\mathbf{q}\to 0} \frac{N\lvert{\mathbf{q}}\rvert}{2mc}. (Used low momentum form of Bogoliubov dispersion) \omega(\mathbf{q})\xrightarrow{\mathbf{q}\to 0} c\lvert{\mathbf{q}}\rvert where c = \sqrt{\frac{n_0U_0}{m}} is the speed of sound)
c.f Gross–Pitaevskii ground state (Poissonian fluctuations) \Braket{0|\rho_{-\mathbf{q}}\rho_{\mathbf{q}}|0} = N
Quantum Depletion
Finite fraction of particles have \mathbf{p}\neq 0. Let’s find \langle N_\mathbf{p}\rangle
N_\mathbf{p}=a^\dagger_{\mathbf{p}}a^{\vphantom{\dagger}}_{\mathbf{p}} in terms of Bogoliubov quasiparticles
a^\dagger_{\mathbf{p}}a^{\vphantom{\dagger}}_{\mathbf{p}}=(b^\dagger_\mathbf{p}\cosh\kappa_{\mathbf{p}}-b^{\vphantom{\dagger}}_{-\mathbf{p}}\sinh\kappa_{\mathbf{p}})(b^{\vphantom{\dagger}}_\mathbf{p}\cosh\kappa_{\mathbf{p}}-b^\dagger_{-\mathbf{p}}\sinh\kappa_{\mathbf{p}})
- Then evaluate expectation
\langle N_\mathbf{p}\rangle=\langle a^\dagger_{\mathbf{p}}a^{\vphantom{\dagger}}_{\mathbf{p}}\rangle = \sinh^2\kappa_{p}\xrightarrow{ \lvert{\mathbf{p}}\rvert\ll \xi^{-1}}\frac{mc_s}{2\lvert{\mathbf{p}}\rvert}
- Radial density distribution 4\pi p^2 N_\mathbf{p} peaked around \xi^{-1}
Fraction of atoms not in the condensate \frac{1}{N}\sum_{\mathbf{p}\neq 0} \langle N_\mathbf{p}\rangle=\frac{8}{3\sqrt{\pi}}\sqrt{n a^3}, Born approximation for scattering length a=\frac{mU_0}{4\pi}
Typical experimental conditions in experiments on ultracold atoms: depletion does not much exceed 0.01, which justifies GP approximation
Liquid He^{4} is an interacting Bose condensate, but depletion is much larger (condensate fraction \sim 10\%). Bogoliubov not accurate here
Applying a lattice can lead to total depletion and a quantum phase transition out of superfluid state